题目内容
已知二次函数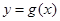 的导函数的图像与直线
的导函数的图像与直线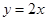 平行,且
平行,且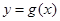 在
在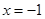 处取得极小值
处取得极小值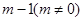 .设
.设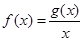 .
.
(1)若曲线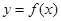 上的点
上的点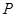 到点
到点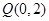 的距离的最小值为
的距离的最小值为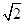 ,求
,求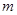 的值;
的值;
(2)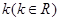 如何取值时,函数
如何取值时,函数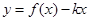 存在零点,并求出零点.
存在零点,并求出零点.
【答案】
(1) ,
,
(2)当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
( ),或
),或 (
( )时,函数
)时,函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点
【解析】
试题分析:解:(1)依题可设 (
( ),
),
则 ;
;
又 的图像与直线
的图像与直线 平行
平行  ,
,
 ,
,  ,
,
设 ,则
,则

当且仅当 时,
时, 取得最小值,即
取得最小值,即 取得最小值
取得最小值
当 时,
时, 解得
解得
当 时,
时, 解得
解得
(2)由 (
( ),得
),得

当 时,方程
时,方程 有一解
有一解 ,函数
,函数 有一零点
有一零点 ;
;
当 时,方程
时,方程 有二解
有二解 ,
,
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
若 ,
, ,
,
函数 有两个零点
有两个零点 ,即
,即 ;
;
当 时,方程
时,方程 有一解
有一解 ,
,  ,
,
函数 有一零点
有一零点
综上,当 时, 函数
时, 函数 有一零点
有一零点 ;
;
当 (
( ),或
),或 (
( )时,
)时,
函数 有两个零点
有两个零点 ;
;
当 时,函数
时,函数 有一零点
有一零点 .
.
考点:函数的零点
点评:主要是考查了函数的零点以及函数的极值的运用,属于中档题。

练习册系列答案
相关题目
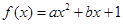 的导函数为
的导函数为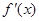 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则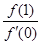 的最小值为 ( )
的最小值为 ( ) 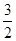 C.3 D.
C.3 D.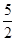
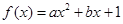 的导函数为
的导函数为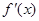 ,
,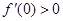 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则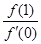 的最小值为( )
的最小值为( )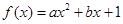 的导函数为
的导函数为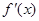 ,
,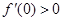 ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则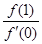 的最小值为 ( )
的最小值为 ( )