题目内容
设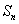 是数列
是数列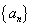 的前
的前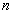 项和,对任意
项和,对任意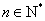 都有
都有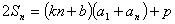 成立, (其中
成立, (其中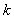 、
、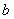 、
、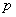 是常数) .
是常数) .
(1)当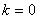 ,
,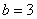 ,
, 时,求
时,求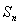 ;
;
(2)当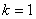 ,
,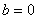 ,
,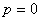 时,
时,
①若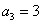 ,
,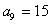 ,求数列
,求数列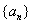 的通项公式;
的通项公式;
②设数列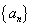 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“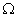 数列”.
数列”.
如果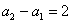 ,试问:是否存在数列
,试问:是否存在数列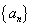 为“
为“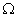 数列”,使得对任意
数列”,使得对任意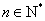 ,都有
,都有
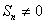 ,且
,且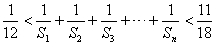 .若存在,求数列
.若存在,求数列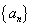 的首项
的首项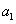 的所
的所
有取值构成的集合;若不存在,说明理由.
解:(1)当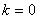 ,
,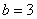 ,
, 时,由
时,由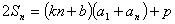 得
得
 ①
①
用 去代
去代 得,
得, , ②
, ②
②—①得, ,
, ,
,
在①中令 得,
得, ,则
,则 0,∴
0,∴ ,
,
∴数列 是以首项为1,公比为3的等比数列,
是以首项为1,公比为3的等比数列,
∴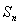 =
=
(2)当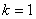 ,
,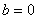 ,
,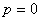 时,
时,
 , ③
, ③
用 去代
去代 得,
得, , ④
, ④
④—③得,  , ⑤
, ⑤
用 去代
去代 得,
得, , ⑥
, ⑥
⑥—⑤得, ,即
,即 ,
,
∴数列 是等差数列.∵
是等差数列.∵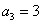 ,
,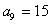 ,
,
∴公差 ,∴
,∴
易知数列 是等差数列,∵
是等差数列,∵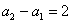 ,∴
,∴ .
.
又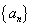 是“
是“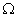 数列”,得:对任意
数列”,得:对任意 ,必存在
,必存在 使
使
 ,
,
得 ,故
,故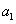 是偶数, …
是偶数, …
又由已知, ,故
,故
一方面,当 时,
时,
 ,对任意
,对任意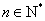 ,
,
都有
另一方面,当 时,
时, ,
, ,
,
则 ,
,
取 ,则
,则 ,不合题意.
,不合题意.
当 时,
时, ,
, ,则
,则

 ,
,
当 时,
时,
 ,
, ,
,
 ,
,
又 ,∴
,∴ 或
或 或
或 或
或
所以,首项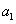 的所有取值构成的集合为
的所有取值构成的集合为

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 },有下列命题
},有下列命题 1, x
1, x
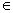 M;②若f (x)=2x,则f (x)
M;②若f (x)=2x,则f (x)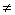 x2),总有
x2),总有 ﹤0成立。
﹤0成立。 (
( 为虚数单位),复数
为虚数单位),复数 ,则一个以
,则一个以 为根的实系数一元二次方程是________.
为根的实系数一元二次方程是________.  ,已知函数
,已知函数 ,若函数
,若函数 恰有两个零点,则
恰有两个零点,则 的取值范围为………( ).
的取值范围为………( ).
 .
. 
 .
. 
 .
. 
 .
. 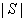 表示集合S中的元素的个数,设
表示集合S中的元素的个数,设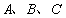 为集合,称
为集合,称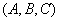 有为有序三元组.如果集合
有为有序三元组.如果集合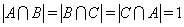 ,且
,且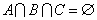 ,则称有序三元组
,则称有序三元组 的子集构成的所有有序三元组中,最小相交的有序三元组的个数为 .
的子集构成的所有有序三元组中,最小相交的有序三元组的个数为 . )是区域
)是区域 内的随机点,函数
内的随机点,函数 在区间[
在区间[ )
) B.
B. C.
C. D.
D.
 满足
满足 ,则( )
,则( ) 有最大值4 B.
有最大值4 B. 有最小值
有最小值
 有最大值
有最大值 D.
D. 有最小值
有最小值