题目内容
设函数f(x)=(1-x)2-ln(1+x),求f(x)的单调区间.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的定义域,求出函数的导数,通过导数与0的关系,求出x的范围即可.
解答:
解:函数f(x)=(1-x)2-ln(1+x)的定义域为(-1,+∞),
∵f′(x)=2(x-1)-
=
,
令f′(x)=0,解得x=1+
,x=1-
当f′(x)>0时,即x>1+
,或-1<x<1-
时,函数f(x)单调递增,
当f′(x)<0时,即1-
<x<1+
时,函数f(x)单调递减,
故函数f(x)=(1+x)2-ln(1+x)在(1-
,1+
)上单调递减,在(-1,1-
)和(1+
,+∞)上单调递增.
∵f′(x)=2(x-1)-
| 1 |
| x+1 |
| 2(x-1)2-1 |
| x+1 |
令f′(x)=0,解得x=1+
| ||
| 2 |
| ||
| 2 |
当f′(x)>0时,即x>1+
| ||
| 2 |
| ||
| 2 |
当f′(x)<0时,即1-
| ||
| 2 |
| ||
| 2 |
故函数f(x)=(1+x)2-ln(1+x)在(1-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查函数的对数求解函数的单调区间的方法,函数的定义域是易错点,易因为忘记求定义域导致错误,考查计算能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
动点E在正方体ABCD-A1B1C1D1的棱BC上,F是CD的中点,则二面角C1-EF-C的余弦值的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
D、(0,
|
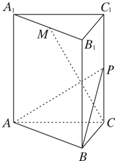 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2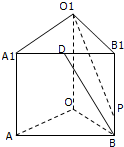 已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为
已知在直三棱柱ABO-A1B1O1中,OO1=4,OA=4,OB=3,∠AOB=90°,点D是线段A1B1的中点,点P是侧棱BB1上一点,若O1P与平面AOB所成的角正切值为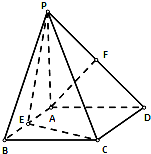 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.