题目内容
设a、b是不相等的实数,试探求证明不等式(a4+b4)(a2+b2)>(a3+b3)2的方法.
答案:
解析:
解析:
探究思路:对于不等式的证明比较常见的方法是作差法,即求出不等式两边式子的差,再根据差与零的关系来达到证明不等式的目的.现在我们又学习了向量数量积的坐标表示,因此可以根据不等式结构构造向量利用向量知识来达到证明不等式的目的.
方法一:(a4+b4)(a2+b2)-(a3+b3)2
=a6+b6+a4b2+a2b4-a6-b6-2a3b3
=a4b2+a2b4-2a3b3
=a2b2(a2-ab)+a2b2(b2-ab)
=a2b2(a-b)2.
由于a、b是不相等的实数,则(a4+b4)(a2+b2)-(a3+b3)2=a2b2(a-b)2>0,
即(a4+b4)(a2+b2)>(a3+b3)2.
方法二:设m=(a2,b2),n=(a,b),
则m·n=a3+b3,
又a、b是不相等的实数,则a2b-ab2≠0,
即向量m、n不共线,所以有|m·n|<|m||n|,即(a4+b4)(a2+b2)>(a3+b3)2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
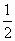 [f(x1)+f(x2)]有不相等的两实根,且必有一根属于(x1、x2);
[f(x1)+f(x2)]有不相等的两实根,且必有一根属于(x1、x2);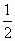 [f(x1)+f(x2)]在(x1、x2)内的实根为m,且x1、m-
[f(x1)+f(x2)]在(x1、x2)内的实根为m,且x1、m-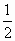 、x2成等差数列,设x=x0是f(x)的对称轴方程.
、x2成等差数列,设x=x0是f(x)的对称轴方程.