题目内容
在△ABC中，O是平面ABC上的一点，动点P满足
=
+λ(
+
)，λ∈R，则点P的轨迹过△ABC的（ ）
| OP |
| OA |
| OB |
| OC |
分析：根据向量的加法的平行四边形法则向量的运算法则，对
=
+λ(
+
)进行化简，得到
=
+λ(
+
)，根据三点共线的充要条件知道P、A、D三点共线，从而得到点P的轨迹一定经过△ABC的重心．
| OP |
| OA |
| OB |
| OC |
| OP |
| OA |
| OB |
| OC |
解答：解：取BC的中点D，则 2
=
+
∵
=
+λ(
+
)
∴
=
+2λ
∴P、A、D三点共线，
∴点P的轨迹一定经过△ABC的重心．
故选B．
| OD |
| OC |
| OB |
∵
| OP |
| OA |
| OB |
| OC |
∴
| OP |
| OA |
| OD |
∴P、A、D三点共线，
∴点P的轨迹一定经过△ABC的重心．
故选B．
点评：此题是个中档题．考查向量的加法法则和运算法则，以及三点共线的充要条件，和三角形的五心问题，综合性强，体现了数形结合的思想．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
与
共线，则存在唯一的实数
，使
共面，则它们所在直线也共面；
上的射影．若PA 、PB、PC两两垂直，则O是△ABC垂心．
三点不共线，
是平面
,则点
一定在平面
，则点O是△ABC的（ ）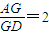
；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
= ．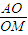