题目内容
（2011•渭南三模）平面上：在正三角形ABC中，若D是BC的中点，G是三角形ABC的重心，则
=2；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
=
| AG |
| GD |
| AO |
| OM |
3
3
．分析：本题考查的知识点是类比推理，由平面图形的性质类比猜想空间几何体的性质，一般的思路是：点到线，线到面，或是二维变三维；由题目中在正三角形ABC中，若D是边BC中点，G是三角形ABC的重心，则
=2中的结论是二维线段长与线段长的关系，类比后的结论应该为三维的边与边的关系．
| AG |
| GD |
解答：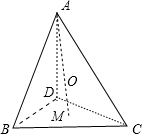
解：由平面图形的性质类比猜想空间几何体的性质，
一般的思路是：点到线，线到面，或是二维变三维；
由题目中“在正三角形ABC中，若D是BC的中点，G是三角形ABC的重心，则
=2”，
我们可以推断：“在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
=3．”
理由如下：
设正四面体ABCD边长为1，易求得AM=
，又O到四面体各面的距离都相等，
所以O为四面体的内切球的球心，设内切球半径为r，
则有r=
，可求得r即OM=
，
所以AO=AM-OM=
，所以
=3．
故答案为：3．
解：由平面图形的性质类比猜想空间几何体的性质，一般的思路是：点到线，线到面，或是二维变三维；
由题目中“在正三角形ABC中，若D是BC的中点，G是三角形ABC的重心，则
| AG |
| GD |
我们可以推断：“在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
| AO |
| OM |
理由如下：
设正四面体ABCD边长为1，易求得AM=
| ||
| 3 |
所以O为四面体的内切球的球心，设内切球半径为r，
则有r=
| 3V |
| S表 |
| ||
| 12 |
所以AO=AM-OM=
| ||
| 4 |
| AO |
| OM |
故答案为：3．
点评：本题考查类比推理知识，由平面到空间的类比是经常考查的知识，要认真体会其中的类比方式．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
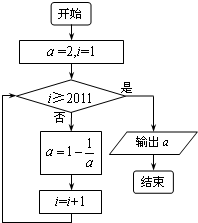（2011•渭南三模）已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
（2011•渭南三模）已知正三棱柱的侧面积为36，其三视图如图所示，则它的左视图的面积为（ ）