题目内容
已知抛物线y=ax2+2x+c与X轴交于A,B两点,顶点为C.在-1,-2,0,1,2中任选一个数记为a,在剩下的数中选一个记为c,使△ABC为等腰直角三角形的概率为
.
| 1 |
| 4 |
| 1 |
| 4 |
分析:由已知得出基本事件的总数,再利用判别式△>0,根与系数的关系,等腰直角三角形的性质得出满足条件的要求事件的基本事件的总数即可.
解答:解:如图所示,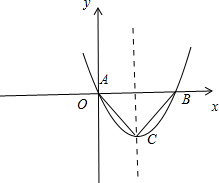 ∵已知抛物线y=ax2+2x+c,∴a≠0.C(-
∵已知抛物线y=ax2+2x+c,∴a≠0.C(-
,
).
在-1,-2,0,1,2中任选一个数记为a,在剩下的数中选一个记为c.
则a,c的选法共有以下16种:-1,-2;-1,0;-1,1;-1,2;-2,-1;-2,0;-2,1;-2,2;1,-1;1,-2;1,0;1,2;2,-1;2,-2;2,0;2,1.
设A(x1,0),B(x2,0).∵抛物线与x轴相较于不同两点,∴△=4-4ac>0,即ac<1.
则x1+x2=-
,x1x2=
.
又若要满足△ABC是等腰直角三角形,则
•
=0,
∴(x1+
,
)•(x2+
,
)=x1x2+
(x1+x2)+
+
=0,代入得
-
+
+
=0.
化为(ac-1)ac=0,∵ac<1,a≠0,∴只有c=0.
而c=0的只有4种情况:-1,0;-2,0;1,0;2,0.
因此使△ABC为等腰直角三角形的概率p=
=
.
故答案为
.
 ∵已知抛物线y=ax2+2x+c,∴a≠0.C(-
∵已知抛物线y=ax2+2x+c,∴a≠0.C(-| 1 |
| a |
| ac-1 |
| a |
在-1,-2,0,1,2中任选一个数记为a,在剩下的数中选一个记为c.
则a,c的选法共有以下16种:-1,-2;-1,0;-1,1;-1,2;-2,-1;-2,0;-2,1;-2,2;1,-1;1,-2;1,0;1,2;2,-1;2,-2;2,0;2,1.
设A(x1,0),B(x2,0).∵抛物线与x轴相较于不同两点,∴△=4-4ac>0,即ac<1.
则x1+x2=-
| 2 |
| a |
| c |
| a |
又若要满足△ABC是等腰直角三角形,则
| CA |
| CB |
∴(x1+
| 1 |
| a |
| 1-ac |
| a |
| 1 |
| a |
| 1-ac |
| a |
| 1 |
| a |
| 1 |
| a2 |
| (1-ac)2 |
| a2 |
| c |
| a |
| 2 |
| a2 |
| 1 |
| a2 |
| (1-ac)2 |
| a2 |
化为(ac-1)ac=0,∵ac<1,a≠0,∴只有c=0.
而c=0的只有4种情况:-1,0;-2,0;1,0;2,0.
因此使△ABC为等腰直角三角形的概率p=
| 4 |
| 16 |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评:正确得出基本事件的总数和利用判别式△>0、根与系数的关系、等腰直角三角形的性质得出满足条件的要求事件的基本事件的总数是解题的关键.

练习册系列答案
相关题目
已知抛物线y=ax2+bx+c与直线y=-bx交于A、B两点,其中a>b>c,a+b+c=0,设线段AB在x轴上的射影为A1B1,则|A1B1|的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(2, 2
|