题目内容
(本小题满分12分)
已知函数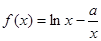 。
。
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)若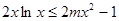 在
在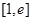 恒成立,求
恒成立,求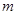 的取值范围。
的取值范围。
解:(Ⅰ)当 时,
时, 单调递减,
单调递减, 单调递增。
单调递增。
当 时,
时, 单调递增。
单调递增。
(Ⅱ) 。
。
解析试题分析: (1)因为 ,然后分母为正,然后确定分子的正负来得到单调区间。
,然后分母为正,然后确定分子的正负来得到单调区间。
(2)要证明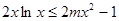 ,得到
,得到
构造函数 ,求解最大值即可。
,求解最大值即可。
解:(Ⅰ)
当 时,
时, 单调递减,
单调递减, 单调递增。
单调递增。
当 时,
时, 单调递增。
单调递增。
(Ⅱ)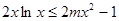 ,得到
,得到
令已知函数


 单调递减,
单调递减, 单调递增。
单调递增。 ,即
,即 ,
,
 在
在 单调递减,
单调递减,
在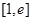 ,
, ,若
,若 恒成立,则
恒成立,则 。
。
考点:本题主要考查了函数与导数的正负的关系,进而确定单调性的运用。
点评:解决该试题的关键是能准确的利用参数的取值范围得到函数的单调性的运用,并且可知函数的最值问题,进而证明不等式的恒成立。

练习册系列答案
相关题目
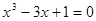 的根一个在
的根一个在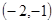 内,一个在
内,一个在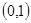 内,一个在
内,一个在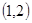 内.(12分)
内.(12分)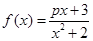 (其中
(其中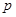 为常数,
为常数,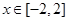 )为偶函数.
)为偶函数. 在
在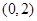 上是单调减函数;
上是单调减函数;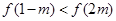 ,求实数
,求实数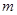 的取值范围.
的取值范围.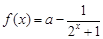 ,
,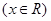 .
. 为何实数
为何实数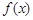 在
在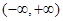 上为增函数;
上为增函数;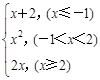 .
.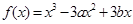
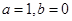 ,求
,求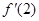 的值;
的值; 的图像与直线
的图像与直线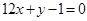 相切于点
相切于点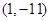 ,求
,求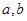 的值;
的值;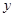 (毫克)与时间
(毫克)与时间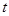 (小时)成正比.药物释放完毕后,
(小时)成正比.药物释放完毕后,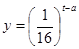 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: