题目内容
已知数列 满足
满足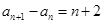 (
(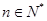 )且
)且
(1)求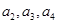 的值
的值
(2)求 的通项公式
的通项公式
(3)令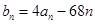 ,求
,求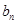 的最小值及此时
的最小值及此时 的值
的值
(1) (2)
(2) (3)
(3)
解析试题分析:(1)因为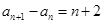 ,且
,且
所以
(2)因为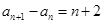 ,所以
,所以 ,
,
这n-1个式子相加可得
(3)由(1)知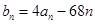

因为 ,结合二次函数的性质可以得到
,结合二次函数的性质可以得到
考点:本小题主要考查累加法求数列的通项公式和数列的函数性质的应用.
点评:数列是一类特殊的函数,所以有时利用函数的性质解决数列问题,不过要注意

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
在等差数列{an}中,a2=1,a4=5,则{an}的前5项和S5=( )
| A.7 | B.15 | C.20 | D.25 |
已知等差数列 的前
的前 项和
项和 满足
满足 且
且 ,则下列结论错误的是( ).
,则下列结论错误的是( ).
A. 和 和 均为 均为 的最大值 的最大值 |
B. |
C.公差 |
D. |
已知等差数列 的前
的前 项和为
项和为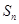 ,
, ,
, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
 的第二、三及第六项构成等比数列,则
的第二、三及第六项构成等比数列,则 = .
= . 满足:
满足: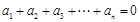 且
且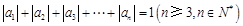 ,则称数列
,则称数列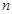 阶“归化数列”.
阶“归化数列”.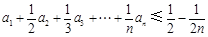 .
.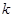 (
(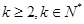 )的数列
)的数列 、
、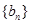 、
、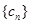 前
前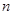 项的和分别为
项的和分别为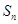 、
、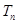 、
、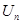 .已知集合
.已知集合 =
=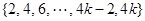 .
.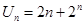 ,求数列
,求数列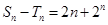
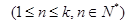 ,试研究
,试研究 和
和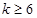 时是否存在符合条件的数列对(
时是否存在符合条件的数列对(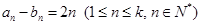 ,对于固定的
,对于固定的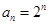 ,把数列
,把数列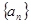 的各项排成如图所示的三角形状,记
的各项排成如图所示的三角形状,记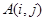 表示第i行中第j个数,则结论
表示第i行中第j个数,则结论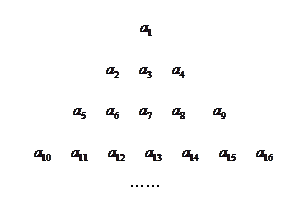
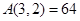 ;
;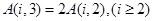 ;
;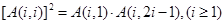 ;
;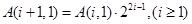 .
.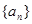 满足:
满足: 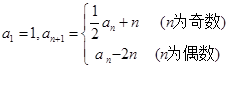
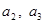 ;
; 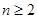 时,求
时,求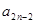 与
与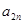 的关系式,并求数列
的关系式,并求数列