题目内容
已知等差数列 的前
的前 项和为
项和为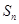 ,
, ,
, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:依题意 ,即
,即 ①,又
①,又 ②,所以①
②,所以① ②,且结合等差数列的性质有
②,且结合等差数列的性质有 ,所以
,所以 ,这样
,这样 ,所以
,所以 ,故选择B,这里巧妙地运用了性质,若回到基本量
,故选择B,这里巧妙地运用了性质,若回到基本量 ,布列方程,从理论上讲可行,实际解时还要注意方法和技巧.
,布列方程,从理论上讲可行,实际解时还要注意方法和技巧.
考点:等差数列通项公式、前 项和公式及性质.
项和公式及性质.

练习册系列答案
相关题目
设等差数列 的公差为d,若数列
的公差为d,若数列 为递减数列,则( ).
为递减数列,则( ).
A. | B. | C. | D. |
设函数 ,则
,则 的值为( ).
的值为( ).
A. | B. | C. | D. |
等差数列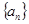 与
与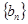 的前
的前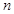 项和分别是
项和分别是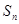 和
和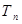 ,已知
,已知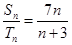 ,则
,则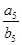 等于( )
等于( )
| A.7 | B.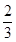 | C.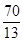 | D.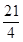 |
设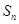 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
设等差数列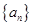 的前n项和为
的前n项和为 ,若
,若 =-2,
=-2, =0,
=0, =3,则m=( )
=3,则m=( )
| A.3 | B.4 | C.5 | D.6 |
等差数列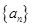 中,a1=1,d=3,an=298,则n的值等于( ).
中,a1=1,d=3,an=298,则n的值等于( ).
| A.98 | B. 100 | C.99 | D.101 |
等差数列 的值为( )
的值为( )
| A.66 | B.99 | C.144 | D.297 |
 满足
满足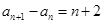 (
(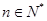 )且
)且
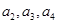 的值
的值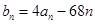 ,求
,求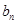 的最小值及此时
的最小值及此时 的值
的值