题目内容
设![]() 为数列
为数列![]() 的前
的前![]() 项和,对任意的
项和,对任意的![]() ,都有
,都有![]()
![]() 为常数,且
为常数,且![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)设数列![]() 的公比
的公比![]() ,数列
,数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(1)证明:当![]() 时,
时,![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() .即
.即![]() .
.
又![]() 为常数,且
为常数,且![]() ,∴
,∴![]()
![]() .
.
![]() ∴数列
∴数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(2)解:由(1)得,![]()
![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]()
![]() .
.
∴![]() 是首项为
是首项为![]() ,公差为1的等差数列.
,公差为1的等差数列.
∴![]() ,即
,即![]() (
(![]() ).
).
(3)解:由(2)知![]() ,则
,则![]() .所以
.所以![]() ,…8分
,…8分
即![]()
![]() , ①
, ①
则![]() , ②
, ②
②-①得![]() ,
,
故![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为数列
为数列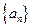 的前
的前 项和,对任意的
项和,对任意的 N
N ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列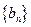 的通项公式;
的通项公式; 的前
的前 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有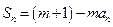
 为常数,且
为常数,且 .
.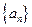 是等比数列;
是等比数列; ,数列
,数列 满足
满足 ,求数列
,求数列 的前
的前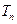 .
. 为数列
为数列 的前
的前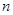 项和,对任意的
项和,对任意的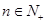 ,都有
,都有 (
(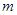 为正常数).
为正常数). 满足
满足 求数列
求数列 的前
的前 .
. 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时, .又数列
.又数列 满足
满足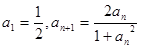 .
. 的表达式;
的表达式; 为数列
为数列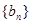 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的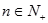 ,都有
,都有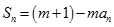
 为常数,且
为常数,且 .
. 是等比数列;
是等比数列; ,数列
,数列 满足
满足 ,求数列
,求数列 的前
的前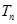 .
.