题目内容
设 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的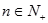 ,都有
,都有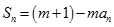
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比 ,数列
,数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和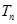 .
.
【答案】
(1)证明:当 时,
时, ,解得
,解得 .…………………1分
.…………………1分
当 时,
时, .即
.即 .………2分
.………2分
又 为常数,且
为常数,且 ,∴
,∴
 . ………………………3分
. ………………………3分
∴数列 是首项为1,公比为
是首项为1,公比为 的等比数列. ……………………4分
的等比数列. ……………………4分
(2)解:由(1)得,
 ,
, . ………………………5分
. ………………………5分
∵ ,∴
,∴ ,即
,即
 . ………7分
. ………7分
∴ 是首项为
是首项为 ,公差为1的等差数列. ………………………………………8分
,公差为1的等差数列. ………………………………………8分
∴ ,即
,即 (
( ). ………………………9分
). ………………………9分
(3)解:由(2)知 ,则
,则 .
.
所以 , ………………10分
, ………………10分
即
 ,
① ……11分
,
① ……11分
则 , ②………12分
, ②………12分
②-①得 ,
……………………13分
,
……………………13分
故 . ………………14分
. ………………14分
【解析】本题主要考查等比数列的性质.当出现等比数列和等差数列相乘的形式时,求和可用错位相减法.
(1)当n≥2时,根据an=Sn-Sn-1,进而得出an和an-1的关系整理得an an-1 =m
an-1 =m (
1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.
(
1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.
(2)根据(1)可得f(m)的解析式.再根据bn=f(bn-1)整理可得(1  bn) -(1
bn) -(1 bn-1)
=1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.
bn-1)
=1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.
(3)把(2)中的bn代入{2n+1  bn },再通过错位相减法求得Tn
bn },再通过错位相减法求得Tn

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 为数列
为数列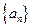 的前
的前 项和,对任意的
项和,对任意的 N
N ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列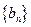 的通项公式;
的通项公式; 的前
的前 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有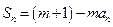
 为常数,且
为常数,且 .
.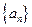 是等比数列;
是等比数列; ,数列
,数列 满足
满足 ,求数列
,求数列 的前
的前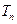 .
. 为数列
为数列 的前
的前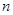 项和,对任意的
项和,对任意的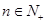 ,都有
,都有 (
(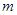 为正常数).
为正常数). 满足
满足 求数列
求数列 的前
的前 .
. 定义在区间
定义在区间 上,
上, ,且当
,且当 时,
时, .又数列
.又数列 满足
满足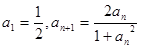 .
. 的表达式;
的表达式; 为数列
为数列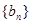 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.