Question

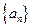（本小题满分14分）设为数列的前项和，对任意的N，都有为常数，且．
（1）求证：数列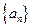是等比数列；
（2）设数列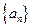的公比，数列满足 ，N，求数列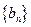的通项公式；
（3）在满足（2）的条件下，求证：数列的前项和．

Answer 1

（本小题满分14分）
（1）证明：当时，，解得．……………………………………1分
当时，．……………………………………………2分
即．
∵为常数，且，∴．………………………………………3分
∴数列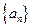是首项为1，公比为的等比数列．………………………………4分
（2）解：由（1）得，，．……………………………5分
∵，…………………………………………………………6分
∴，即．………………………………………………7分
∴是首项为，公差为1的等差数列．…………………………………………8分
∴，即（N）．…………………………………………9分
（3）证明：由（2）知，则．……………………………10分
所以 ，……………………11分
当时，，………………………………………12分
所以

．………………………………………………………14分

解析