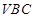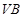题目内容
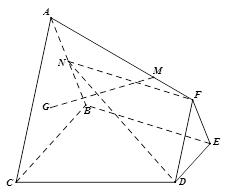
(本题满分14分)如图,已知平面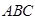
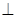 平面
平面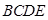 ,
, 与
与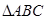 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,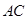 //
//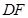 ,四边形
,四边形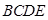 为直角梯形,
为直角梯形,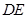 //
//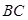 ,
,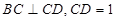 ,点
,点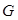 为
为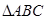 的重心,
的重心,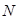 为
为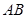 中点,
中点,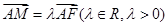 ,
,
(Ⅰ)当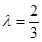 时,求证:
时,求证: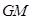 //平面
//平面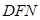
(Ⅱ)若直线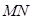 与
与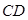 所成角为
所成角为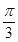 ,试求二面角
,试求二面角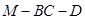 的余弦值.
的余弦值.
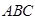
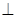 平面
平面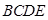 ,
, 与
与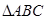 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,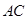 //
//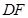 ,四边形
,四边形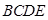 为直角梯形,
为直角梯形,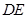 //
//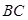 ,
,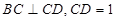 ,点
,点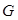 为
为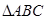 的重心,
的重心,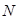 为
为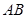 中点,
中点,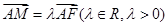 ,
,
(Ⅰ)当
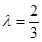 时,求证:
时,求证: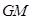 //平面
//平面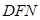
(Ⅱ)若直线
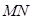 与
与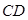 所成角为
所成角为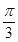 ,试求二面角
,试求二面角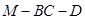 的余弦值.
的余弦值.(Ⅰ)见解析;(Ⅱ)二面角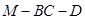 的余弦值
的余弦值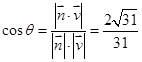 .
.
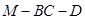 的余弦值
的余弦值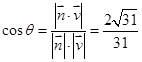 .
.(1)只须证:连接AG并延长交CE于P点,连接PB,PD,易证NPDF为平行四边形,然后根据平行线分分段成比例关系证DM//PF即可.
(2) 由于本小题建系比较容易,所以易采用空间向量法求二面角即可.先求出二面角两个面的法向量,然后根据法向量的夹角与二面角相等或互补进行计算.
(Ⅰ)连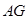 延长交
延长交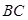 于
于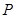 ,
,

因为点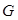 为
为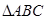 的重心,所以
的重心,所以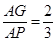
又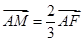 ,所以
,所以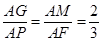 ,所以
,所以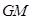 //
//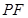 ;
;
因为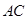 //
//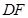 ,
,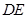 //
//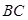 ,所以平面
,所以平面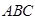 //平面
//平面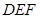 ,
,
又 与
与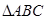 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,
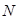 为
为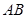 中点,
中点,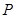 为
为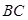 中点,
中点, 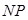 //
//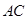 ,又
,又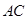 //
//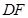 ,
,
所以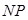 //
//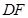 ,得
,得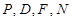 四点共面
四点共面
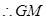 //平面
//平面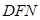
(Ⅱ)平面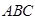
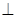 平面
平面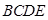 ,易得平面
,易得平面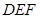
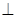 平面
平面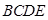 ,
,
以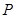 为原点,
为原点, 为x轴,
为x轴,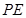 为y轴,
为y轴,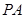 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,
则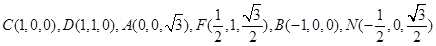 ,设
,设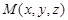 ,
,
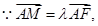
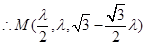 ,
,
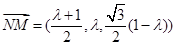 ,
,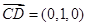
因为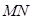 与
与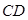 所成角为
所成角为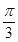 ,所以
,所以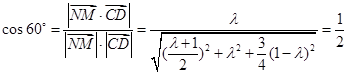 ,
,
得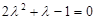 ,
,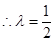 ,
,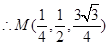 ,
,
设平面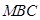 的法向量
的法向量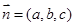 ,则
,则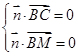 ,取
,取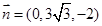 ,
,
面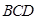 的法向量
的法向量 ,
,
所以二面角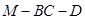 的余弦值
的余弦值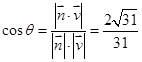 .
.
(2) 由于本小题建系比较容易,所以易采用空间向量法求二面角即可.先求出二面角两个面的法向量,然后根据法向量的夹角与二面角相等或互补进行计算.
(Ⅰ)连
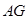 延长交
延长交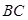 于
于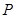 ,
,
因为点
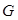 为
为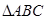 的重心,所以
的重心,所以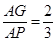
又
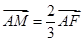 ,所以
,所以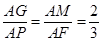 ,所以
,所以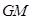 //
//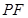 ;
;因为
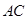 //
//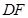 ,
,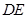 //
//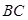 ,所以平面
,所以平面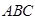 //平面
//平面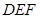 ,
,又
 与
与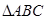 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,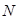 为
为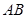 中点,
中点,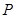 为
为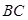 中点,
中点, 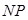 //
//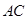 ,又
,又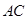 //
//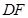 ,
,所以
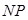 //
//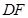 ,得
,得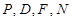 四点共面
四点共面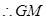 //平面
//平面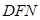
(Ⅱ)平面
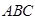
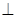 平面
平面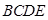 ,易得平面
,易得平面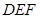
 平面
平面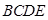 ,
,以
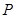 为原点,
为原点, 为x轴,
为x轴,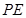 为y轴,
为y轴,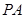 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,则
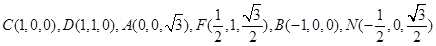 ,设
,设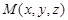 ,
,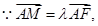
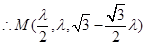 ,
,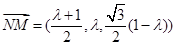 ,
,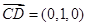
因为
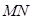 与
与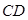 所成角为
所成角为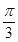 ,所以
,所以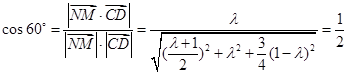 ,
,得
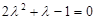 ,
,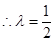 ,
,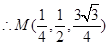 ,
,设平面
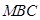 的法向量
的法向量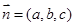 ,则
,则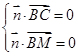 ,取
,取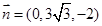 ,
,面
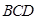 的法向量
的法向量 ,
,所以二面角
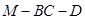 的余弦值
的余弦值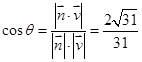 .
.
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 的长;
的长;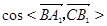 的值;
的值;
 中,
中, 分别是
分别是 的中点,
的中点, 分
分 的中点,
的中点,

 面
面 ;
; 的大小。
的大小。 的体积。
的体积。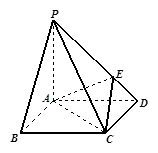
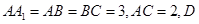 是
是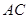 中点.
中点.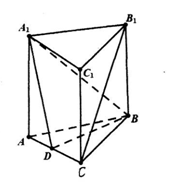
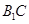 //平面
//平面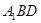 ;
;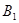 到平面
到平面 的余弦值.
的余弦值. 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.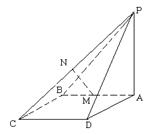
 是
是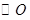 的直径,点
的直径,点 是
是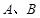 重合),过动点
重合),过动点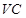 垂直于
垂直于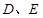 分别是
分别是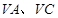 的中点,则下列结论错误的是
的中点,则下列结论错误的是 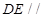 平面
平面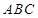
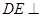 平面
平面