题目内容
设曲线f(x)=acosx+bsinx的一条对称轴为x=
,则曲线y=f(
-x)的一个对称点为( )
| π |
| 5 |
| π |
| 10 |
A.(
| B.(
| C.(
| D.(
|
曲线f(x)=acosx+bsinx=
sin(x+θ),tanθ=
,
所以函数的周期为:2π.因为曲线f(x)=acosx+bsinx的一条对称轴为x=
,
所以函数的一个对称点为:(
-
,0),即(-
,0).
函数y=f(-x)的一个对称中心为(
,0),
y=f(
-x)的图象可以由函数y=f(-x)的图象向右平移
单位得到的,
所以曲线y=f(
-x)的一个对称点为(
+
,0),即(
,0).
故选B.
| a2+b2 |
| a |
| b |
所以函数的周期为:2π.因为曲线f(x)=acosx+bsinx的一条对称轴为x=
| π |
| 5 |
所以函数的一个对称点为:(
| π |
| 5 |
| π |
| 2 |
| 3π |
| 10 |
函数y=f(-x)的一个对称中心为(
| 3π |
| 10 |
y=f(
| π |
| 10 |
| π |
| 10 |
所以曲线y=f(
| π |
| 10 |
| 3π |
| 10 |
| π |
| 10 |
| 2π |
| 5 |
故选B.

练习册系列答案
相关题目
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分. (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分.) ,求M﹣1.
,求M﹣1.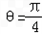 (ρ∈R),它与曲线C
(ρ∈R),它与曲线C (
(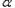 为参数)相较于A、B两点,求AB的长.
为参数)相较于A、B两点,求AB的长.
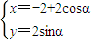 (α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
(α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
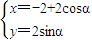 (α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
(α为参数),若以点O(0,0)为极点,x正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .