Question

（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）
A．设函数f（x）=|2x+1|-|x-4|．则不等式f（x）＞2的解集为    ；
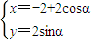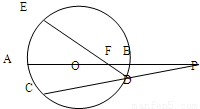
B．（坐标系与参数方程选做题）曲线C：（α为参数），若以点O（0，0）为极点，x正半轴为极轴建立极坐标系，则该曲线的极坐标方程是    ．

C．（几何证明选讲选做题） 如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，弧AE=弧AC，DE交AB于F，且AB=2BP=4，则PF=    ．

Answer 1

【答案】分析：A，通过对x分类讨论去掉绝对值符号即可求得分段函数f（x）的表达式，从而可|求得不等式f（x）＞2的解集；
B，根据题意可以点O（0，0）为极点，x正半轴为极轴建立极坐标系作出图形，从而得到该曲线的极坐标方程；
C：由于点F在直径AB上，可构造相似形，利用割线定理转化求解．
解答：解：对于A，∵f（x）=|2x+1|-|x-4|=，
∴当x＜-时，f（x）＞2?-x-5＞2，
∴x＜-7；
当-≤x≤4时，f（x）＞2?3x-3＞2，
∴＜x≤4；
当x＞4时，f（x）＞2?x+5＞2，
∴x＞4；
综上所述，不等式f（x）＞2的解集为{x|x＜-7或x＞}；
对于B，由参数方程得其普通方程为：（x+2）²+y²=4，
∴以点O（0，0）为极点，x正半轴为极轴建立极坐标系，

则该曲线的极坐标方程是ρ=4cos（π-θ）=-4cosθ；
对于C，连接OC，

∵∠AOC的度数=弧AC的度数，∠EDC的度数=弧EC的度数=弧AC的度数
∴∠AOC=∠EDC，
∴∠POC=∠PDF，
∴△POC∽△PDF
∴=，
即PF===2×=3．
故答案为：A，{x|x＜-7或x＞}；B，ρ=-4cosθ；C，3．
点评：本题A考查绝对值不等式的解法，通过对x分类讨论去掉绝对值符号是关键；B考查简单曲线的极坐标方程，将参数方程转化为极坐标方程是关键，C考查几何证明，构造解决问题的相似三角形是关键，利用切割线定理转化是难点，属于中档题．