题目内容
集合 ,B={y|y=asinθ,
,B={y|y=asinθ, ,a>0}
,a>0}
(1)求集合A和B;
(2)若A∩B=∅,求a的取值范围.
解:(1)由集合A中的不等式变形得: ≥0,
≥0,
可化为(x-4)(x+3)≥0,且x+3≠0,
解得:x≥4或x<-3,
∴A=(-∞,-3)∪[4,+∞);
由集合B中的函数y=asinθ(a>0),θ∈[- ,
, ],得到-
],得到- ≤sinθ≤1,
≤sinθ≤1,
∴- a≤y=asinθ≤a,
a≤y=asinθ≤a,
∴B=[- a,a];
a,a];
(2)∵A∩B=∅,
∴ ,
,
解得:a<4,
则a的范围为a<4.
分析:(1)将集合A中的不等式移项变形后,根据两数相乘积为正,得到两因式同号,求出不等式的解集得出x的范围,确定出集合A,由角的范围,利用正弦函数的图象与性质求出集合B中函数的值域,确定出B;
(2)由两集合的交集为空集,列出关于m的不等式组,求出不等式组的解集即可得到a的范围.
点评:此题属于以其他不等式的解法、三角函数的值域为平台,考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
 ≥0,
≥0,可化为(x-4)(x+3)≥0,且x+3≠0,
解得:x≥4或x<-3,
∴A=(-∞,-3)∪[4,+∞);
由集合B中的函数y=asinθ(a>0),θ∈[-
 ,
, ],得到-
],得到- ≤sinθ≤1,
≤sinθ≤1,∴-
 a≤y=asinθ≤a,
a≤y=asinθ≤a,∴B=[-
 a,a];
a,a];(2)∵A∩B=∅,
∴
 ,
,解得:a<4,
则a的范围为a<4.
分析:(1)将集合A中的不等式移项变形后,根据两数相乘积为正,得到两因式同号,求出不等式的解集得出x的范围,确定出集合A,由角的范围,利用正弦函数的图象与性质求出集合B中函数的值域,确定出B;
(2)由两集合的交集为空集,列出关于m的不等式组,求出不等式组的解集即可得到a的范围.
点评:此题属于以其他不等式的解法、三角函数的值域为平台,考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
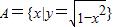 ,B={y|y=x2+1},则A∩B= .
,B={y|y=x2+1},则A∩B= . ,B={y|y=lg(x2+1)},则(CUA)∩B=( )
,B={y|y=lg(x2+1)},则(CUA)∩B=( ) ,B={y|y=2x},则A∩B=( )
,B={y|y=2x},则A∩B=( ) ,B={y|y=x2-1,x∈R},则A∩B=( )
,B={y|y=x2-1,x∈R},则A∩B=( )


