题目内容
集合
，B={y|y=x2-1，x∈R}，则A∩B=（ ）A．
B．
C．
D．
【答案】分析：分别求出集合A中函数的定义域和集合B中函数的值域得到集合A和B，求出交集即可．
解答：解：由集合A中的函数y=
有意义得3-x2≥0，解得-
≤x≤
，所以集合A=[-
，
]；
由集合B中函数y=x2-1的值域为y≥-1，得到集合B=[-1，+∞），
则A∩B={Z|-1≤z≤
}
故选C
点评：此题属于以函数的定义域和值域为平台，求集合交集的基础题，也是高考常考的题型．
解答：解：由集合A中的函数y=
有意义得3-x2≥0，解得-≤x≤，所以集合A=[-，]；由集合B中函数y=x2-1的值域为y≥-1，得到集合B=[-1，+∞），
则A∩B={Z|-1≤z≤
}故选C
点评：此题属于以函数的定义域和值域为平台，求集合交集的基础题，也是高考常考的题型．
练习册系列答案
相关题目
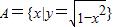，B={y|y=x2+1}，则A∩B= ．
，B={y|y=lg（x2+1）}，则（CUA）∩B=（ ）
，B={y|y=2x}，则A∩B=（ ）