题目内容
已知A={x|(log2x)2-log2x＜0}，B={x|x2-2ax+a2-1＞0}，且A⊆B，求实数a的取值范围．
分析：先分别化简A，B，然后利用A⊆B，求实数a的取值范围．
解答：解：由题意得：A={x|0＜log2x＜1}={x|1＜x＜2}．
B={x|[x-（a-1）][x-（a+1）]＞0}={x|x＞a+1或x＜a-1}，
∵A⊆B
∴2≤a-1或a+1≤1，
∴a≥3或a≤0．
B={x|[x-（a-1）][x-（a+1）]＞0}={x|x＞a+1或x＜a-1}，
∵A⊆B
∴2≤a-1或a+1≤1，
∴a≥3或a≤0．
点评：本题主要考查了利用集合的关系确定参数问题，比较基础．
练习册系列答案
相关题目
(a>0
(a>0
[a2x+2（ab）x-b2x+1]（a、b∈R+），如何求使y为负值的x的取值范围？
(x+y+4)<lo
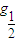[a2x+2（ab）x-b2x+1]（a、b∈R+），如何求使y为负值的x的取值范围？