题目内容
已知y=lo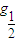 [a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
[a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
【答案】分析:要使y<0,必须a2x+2(ab)x-b2x+1>1,即a2x+2(ab)x-b2x>0.推导出( )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)后,再分
-1(舍去)后,再分 >1,
>1, =1,
=1, <1三种情况进行讨论,从而求出使y为负值的x的取值范围.
<1三种情况进行讨论,从而求出使y为负值的x的取值范围.
解答:解:要使y<0,必须a2x+2(ab)x-b2x+1>1,即a2x+2(ab)x-b2x>0
∵b2x>0
∴( )2x+2(
)2x+2( )x-1>0
)x-1>0
∴( )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)
-1(舍去)
∵a、b∈R+,∴ .
.
当 >1时,即a>b>0时,x>lo
>1时,即a>b>0时,x>lo (
( -1).
-1).
当 =1时,即a=b>0时,x∈R.
=1时,即a=b>0时,x∈R.
当 <1时,即0<a<b时,x<lo
<1时,即0<a<b时,x<lo (
( -1)
-1)
故当a>b>0时,x>lo (
( -1);当a=b>0时,x∈R;当0<a<b时,x<lo
-1);当a=b>0时,x∈R;当0<a<b时,x<lo (
( -1).
-1).
点评:本题是求对数函数取负值时x的取值范围,解题要根据对数函数的性质进行合理转化,然后再分情况进行讨论.
 )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)后,再分
-1(舍去)后,再分 >1,
>1, =1,
=1, <1三种情况进行讨论,从而求出使y为负值的x的取值范围.
<1三种情况进行讨论,从而求出使y为负值的x的取值范围.解答:解:要使y<0,必须a2x+2(ab)x-b2x+1>1,即a2x+2(ab)x-b2x>0
∵b2x>0
∴(
 )2x+2(
)2x+2( )x-1>0
)x-1>0∴(
 )x>
)x> -1或(
-1或( )x<-
)x<- -1(舍去)
-1(舍去)∵a、b∈R+,∴
 .
.当
 >1时,即a>b>0时,x>lo
>1时,即a>b>0时,x>lo (
( -1).
-1).当
 =1时,即a=b>0时,x∈R.
=1时,即a=b>0时,x∈R.当
 <1时,即0<a<b时,x<lo
<1时,即0<a<b时,x<lo (
( -1)
-1)故当a>b>0时,x>lo
 (
( -1);当a=b>0时,x∈R;当0<a<b时,x<lo
-1);当a=b>0时,x∈R;当0<a<b时,x<lo (
( -1).
-1).点评:本题是求对数函数取负值时x的取值范围,解题要根据对数函数的性质进行合理转化,然后再分情况进行讨论.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 [a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
[a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?