题目内容
圆O1:x2+y2=4和圆O2:(x-3)2+y2=4的位置关系是( )
| A、相离 | B、相交 | C、外切 | D、内切 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:由圆的标准方程求出两圆的圆心距d,再根据d大于半径之差而小于半径之和,可得两个圆相交.
解答:
解:圆O1:x2+y2=4和圆O2:(x-3)2+y2=4两个圆的半径都是2,
圆心分别为(0,0)、(3,0),
圆心距为d=3,显然,d大于半径之差而小于半径之和,故两个圆相交,
故选:B.
圆心分别为(0,0)、(3,0),
圆心距为d=3,显然,d大于半径之差而小于半径之和,故两个圆相交,
故选:B.
点评:本题主要考查圆的标准方程,两个圆的位置关系的判定方法,属于基础题.

练习册系列答案
相关题目
给定函数①y=x
,②y=log
x,③y=|x-1|,④y=2x,其中在区间(0,1)上单调递减的函数序号是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①② | B、②③ | C、③④ | D、①④ |
已知全集U={-1,0,1,3},N={0,1,3},则∁UN=( )
| A、{3} | B、{0,1} |
| C、{-1} | D、{-1,3} |
已知向量
=(3,4),
=(-1,2),则
=( )
| AB |
| AC |
| CB |
| A、(4,2) |
| B、(2,6) |
| C、(5,3) |
| D、(-1,5) |
已知sinα>0,cosα>0,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知f(x)是定义在R上的函数,满足f(x)+f(-x)=0,f(x-1)=f(x+1),当x∈[0,1),f(x)=
,函数f(x)的最小值为( )
| 2x |
| 4x+1 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
命题“对任意x∈R,总有x2+1>0”的否定是( )
| A、“对任意x∉R,总有x2+1>0” |
| B、“对任意x∈R,总有x2+1≤0” |
| C、“存在x∈R,使得x2+1>0” |
| D、“存在x∈R,使得x2+1≤0” |
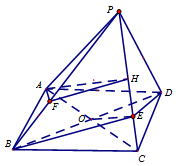 四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,
四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,