题目内容
若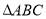 的内角
的内角 所对的边
所对的边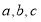 满足
满足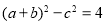 ,且
,且 ,则
,则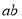 的值为 .
的值为 .

【解析】
试题分析:因为 ,所以由余弦定理可得
,所以由余弦定理可得 即
即 ,又由
,又由 ,所以
,所以 .
.
考点:余弦定理.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
若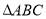 的内角
的内角 所对的边
所对的边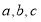 满足
满足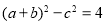 ,且
,且 ,则
,则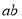 的值为 .
的值为 .

【解析】
试题分析:因为 ,所以由余弦定理可得
,所以由余弦定理可得 即
即 ,又由
,又由 ,所以
,所以 .
.
考点:余弦定理.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案