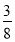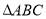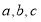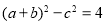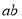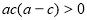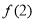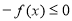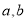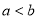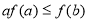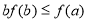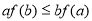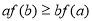题目内容
在锐角
中,角
,
,
对应的边分别是, ,.已知
.
（1）求角
的大小；
（2）若的面积
,
,求
的值.
（1）
；（2）
.
【解析】
试题分析：（1）把已知的等式变形为: 
，并利用正弦定理化简，根据
不为0，可得出
的值，由三角形为锐角三角形，得出
为锐角，利用特殊角的三角函数值即可求出
的度数；（2）由面积公式
求得
，由余弦定理
计算出
，由
计算出
，最后由正弦定理化简
，代入数值即可得到结果.
试题解析：(1)由
可得，而
，所以
因为
为三角形的内角，所以
，所以由可得
又因为
为锐角三角形，所以
，所以 6分
(2)
,由余弦定理得:
由正弦定理可知
或
12分.
考点：正余弦定理在解三角形中的应用，面积公式.
练习册系列答案
相关题目
