题目内容
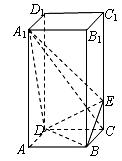
如图,正四棱柱![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求点A到平面![]() 的距离
的距离![]() ;
;
(3)求二面角![]() 的大小.
的大小.
解:
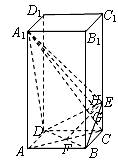
依题设,![]() ,
,![]() .
.
(1)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() .由三垂线定理知,
.由三垂线定理知,![]() .
.
在平面![]() 内,连结
内,连结![]() 交
交![]() 于点
于点![]() ,由于
,由于![]() ,
,
故![]() ,
,![]() ,
,
![]() 与
与![]() 互余.于是
互余.于是![]() .
.
![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() 都垂直,
都垂直,
所以![]()
![]() 平面
平面![]() .
.
(2)![]()
等腰三角形![]() 底边
底边![]() 上的高
上的高![]()
![]()
![]()
![]()
(3)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .由三垂线定理知
.由三垂线定理知![]() ,
,
故![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.![]() .
.
所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 中,
中,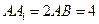 ,点
,点 在
在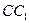 上且
上且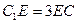
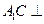 平面
平面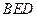 ;(2)求二面角
;(2)求二面角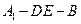 的余弦值
的余弦值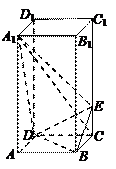
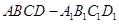 中,
中,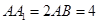 ,点
,点 在
在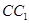 上且
上且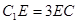
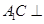 平面
平面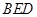 ;
;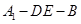 的余弦值.
的余弦值.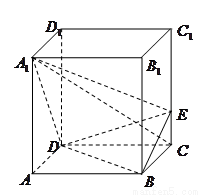
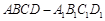 中,设
中,设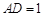 ,
,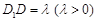 ,
,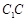 上存在点
上存在点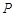 满足
满足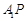
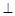 平面
平面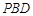 ,求实数
,求实数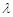 的取值范围
的取值范围