题目内容
如图,在半径为 cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,按如图截出一个内接矩形,则矩形的面积为 cm2.
cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,按如图截出一个内接矩形,则矩形的面积为 cm2.
【答案】分析:过B作BM⊥AO,交FC于点N,交AO于点M,由在半径为 cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,知∠DOC=∠BOC=30°,FC=OF.由CD⊥AO,知
cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,知∠DOC=∠BOC=30°,FC=OF.由CD⊥AO,知 .在△BMO中,∠BOM=60°,∠BMO=90°,OB=
.在△BMO中,∠BOM=60°,∠BMO=90°,OB= ,所以∠OBM=30°,
,所以∠OBM=30°, ,BM=
,BM= ,
, .设FN=x,则BF=2x,则
.设FN=x,则BF=2x,则 ,BF=2x=
,BF=2x= ,由此能求出矩形的面积.
,由此能求出矩形的面积.
解答:解:过B作BM⊥AO,交FC于点N,交AO于点M,
∵在半径为 cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,
cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,
∴∠DOC=∠BOC=30°,
∵CD⊥AO,
∴ ,
,
∵FC∥OA,
∴∠FCO=∠AOC=30°,
∴∠FOC=∠FCO=30°,
∴FC=OF.
在△BMO中,
∵∠BOM=60°,∠BMO=90°,OB= ,
,
∴∠OBM=30°,

∴ ,
,
∴BM= =
= .
.
∴ .
.
设FN=x,则BF=2x,
∴ ,
,
解得 ,
,
∴BF=2x= ,
,
∴ ,
,
∴矩形的面积S= .
.
故答案为: .
.
点评:本题考查三角函数模型的应用问题,是中档题.解题时要认真审题,注意垂径定理、勾股定理、有一个角是30°角的直角三角形的性质的灵活运用,合理地进行等价转化.
 cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,知∠DOC=∠BOC=30°,FC=OF.由CD⊥AO,知
cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,知∠DOC=∠BOC=30°,FC=OF.由CD⊥AO,知 .在△BMO中,∠BOM=60°,∠BMO=90°,OB=
.在△BMO中,∠BOM=60°,∠BMO=90°,OB= ,所以∠OBM=30°,
,所以∠OBM=30°, ,BM=
,BM= ,
, .设FN=x,则BF=2x,则
.设FN=x,则BF=2x,则 ,BF=2x=
,BF=2x= ,由此能求出矩形的面积.
,由此能求出矩形的面积.解答:解:过B作BM⊥AO,交FC于点N,交AO于点M,
∵在半径为
 cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,
cm,圆心角为60°的扇形OAB中,点C为弧AB的中点,∴∠DOC=∠BOC=30°,
∵CD⊥AO,
∴
 ,
,∵FC∥OA,
∴∠FCO=∠AOC=30°,
∴∠FOC=∠FCO=30°,
∴FC=OF.
在△BMO中,
∵∠BOM=60°,∠BMO=90°,OB=
 ,
,∴∠OBM=30°,

∴
 ,
,∴BM=
 =
= .
.∴
 .
.设FN=x,则BF=2x,
∴
 ,
,解得
 ,
,∴BF=2x=
 ,
,∴
 ,
,∴矩形的面积S=
 .
.故答案为:
 .
.点评:本题考查三角函数模型的应用问题,是中档题.解题时要认真审题,注意垂径定理、勾股定理、有一个角是30°角的直角三角形的性质的灵活运用,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
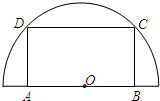 (2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
(2013•闵行区二模)如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.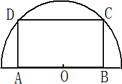
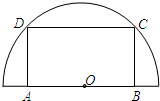 如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.