题目内容
18. 如图,在四棱O-ABCD锥中,底面ABCD四边长为4的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
如图,在四棱O-ABCD锥中,底面ABCD四边长为4的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.(1)证明:直线MN∥平面OCD;
(2)求点B到平面OCD的距离.
分析 (1)取OB中点E,连接ME,NE,证明平面MNE∥平面OCD,即可得到MN∥平面OCD;
(2)利用VB-OCD=V0-BCD,求点B到平面OCD的距离.
解答  (1)证明:取OB中点E,连接ME,NE
(1)证明:取OB中点E,连接ME,NE
∵ME∥AB,AB∥CD,∴ME∥CD
又∵NE∥OC,∴平面MNE∥平面OCD,
MN?平面MNE,
∴MN∥平面OCD;
(2)解:VB-OCD=V0-BCD
∵$AC=4∴OC=2\sqrt{5},OD=2\sqrt{5}$
所以CD边上的高等于4,S△OCD=8,${S_{△BCD}}=4\sqrt{3}$
∴$\frac{1}{3}×8×h=\frac{1}{3}×4\sqrt{3}×2$,∴$h=\sqrt{3}$.
点评 本题考查线面平行的判定,考查点到平面距离的计算,考查学生转化问题的能力,属于中档题.

练习册系列答案
相关题目
8.已知集合M={a,b,c},N={d,e},则从集合M到N可以建立不同的映射个数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”的第二步是( )
| A. | 证明假设n=k(k≥1且k∈N)时正确,可推出n=k+1正确 | |
| B. | 证明假设n=2k+1(k≥1且k∈N)时正确,可推出n=2k+3正确 | |
| C. | 证明假设n=2k-1(k≥1且k∈N)时正确,可推出n=2k+1正确 | |
| D. | 证明假设n≤k(k≥1且k∈N)时正确,可推出n=k+2时正确 |
 过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点
过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点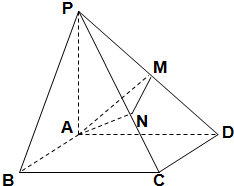 四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M,N分别在侧棱PD,PC上,且$\overrightarrow{PM}=\overrightarrow{MD}$.
四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,且PA=AD=2AB,点M,N分别在侧棱PD,PC上,且$\overrightarrow{PM}=\overrightarrow{MD}$.