题目内容
公比为2的等比数列{an}的各项都是正数，且a5a9=16，则log2a10=（ ）
| A、4 | B、5 | C、6 | D、7 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用等比数列的性质求得a7的值，进而求出结果．
解答：
解：∵a5a9=16，∴a72=16，
∵an＞0，∴a7=4．
∴a10=a7q3=4×23=25，
∴log2a10=5，
故选：B．
∵an＞0，∴a7=4．
∴a10=a7q3=4×23=25，
∴log2a10=5，
故选：B．
点评：本题主要考查等比数列的定义和性质应用，求得a7=4，是解题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
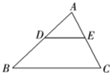如图，已知D、E分别是△ABC的AB、AC边上一点，DE∥BC，且S△ADE：S四边形DBCE=1：3，那么AD：AB等于（ ）A、1：
| ||
| B、1：2 | ||
| C、1：3 | ||
| D、1：4 |
由一组数据（x1，y1），（x2，y2），…，（xn，yn）得到的回归直线方程
=
x+
，那么下面说法不正确的是（ ）
 |
| y |
|
| b |
|
| a |
A、直线
| ||||||||||||||||||||
B、直线
| ||||||||||||||||||||
C、直线
| ||||||||||||||||||||
D、直线
|
（1-ax+by）n展开式中不含x的项的系数绝对值的和为243，不含y的项的系数绝对值的和为32，则a，b，n的值可能为（ ）
| A、a=2，b=-1，n=5 |
| B、a=-1，b=2，n=6 |
| C、a=-1，b=2，n=5 |
| D、a=-2，b=-1，n=6 |
在△ABC中，AB=3，AC=2，BC=
，则
•
等于（ ）
| 5 |
| AB |
| AC |
| A、2 | B、4 | C、3 | D、5 |
设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若
=λ
（λ∈R），
=μ
（μ∈R），且
+
=2，则称A3，A4调和分割A1，A2，已知点C（c，0），D（d，0）（c，d∈R）调和分割点A（0，0），B（1，0），则下面说法正确的是（ ）
| A1A3 |
| A1A2 |
| A1A4 |
| A1A2 |
| 1 |
| λ |
| 1 |
| μ |
| A、C可能是线段AB的中点 |
| B、D可能是线段AB的中点 |
| C、C，D可能同时在线段AB上 |
| D、C，D不可能同时在线段AB的延长线上 |