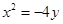题目内容
已知双曲线C 2x2-y2=2与点P(1,2)
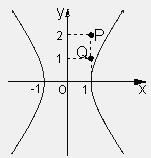
(1)求过P(1,2)点的直线l的斜率取值范围,使l与C分别有一个交点,两个交点,没有交点
(2)若Q(1,1),试判断以Q为中点的弦是否存在

(1)求过P(1,2)点的直线l的斜率取值范围,使l与C分别有一个交点,两个交点,没有交点
(2)若Q(1,1),试判断以Q为中点的弦是否存在
(1) 当k=± ,或k=
,或k=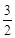 ,或k不存在时,l与C只有一个交点;当
,或k不存在时,l与C只有一个交点;当 <k<
<k<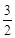 ,或-
,或- <k<
<k< ,或k<-
,或k<- 时,l与C有两个交点;当k>
时,l与C有两个交点;当k>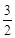 时,l与C没有交点
时,l与C没有交点
(2)不存在
 ,或k=
,或k=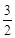 ,或k不存在时,l与C只有一个交点;当
,或k不存在时,l与C只有一个交点;当 <k<
<k<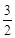 ,或-
,或- <k<
<k< ,或k<-
,或k<- 时,l与C有两个交点;当k>
时,l与C有两个交点;当k>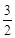 时,l与C没有交点
时,l与C没有交点(2)不存在
【错解分析】第一问,求二次方程根的个数,忽略了二次项系数的讨论 第二问,算得以Q为中点弦的斜率为2,就认为所求直线存在了
【正解】(1)当直线l的斜率不存在时,l的方程为x=1,与曲线C有一个交点 当l的斜率存在时,设直线l的方程为y-2=k(x-1),代入C的方程,并整理得
(2-k2)x2+2(k2-2k)x-k2+4k-6=0 (*)
(ⅰ)当2-k2=0,即k=±
 时,方程(*)有一个根,l与C有一个交点
时,方程(*)有一个根,l与C有一个交点(ⅱ)当2-k2≠0,即k≠±
 时Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k)
时Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k)①当Δ=0,即3-2k=0,k=
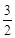 时,方程(*)有一个实根,l与C有一个交点
时,方程(*)有一个实根,l与C有一个交点 ②当Δ>0,即k<
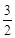 ,又k≠±
,又k≠± ,故当k<-
,故当k<- 或-
或- <k<
<k< 或
或 <k<
<k<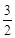 时,方程
时,方程(*)有两不等实根,l与C有两个交点
③当Δ<0,即k>
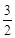 时,方程(*)无解,l与C无交点
时,方程(*)无解,l与C无交点 综上知 当k=±
 ,或k=
,或k=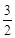 ,或k不存在时,l与C只有一个交点;当
,或k不存在时,l与C只有一个交点;当 <k<
<k<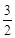 ,或-
,或- <k<
<k< ,或k<-
,或k<- 时,l与C有两个交点;当k>
时,l与C有两个交点;当k>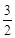 时,l与C没有交点
时,l与C没有交点 (2)假设以Q为中点的弦存在,设为AB,且A(x1,y1),B(x2,y2),则2x12-y12=2,2x22-y22=2两式相减得 2(x1-x2)(x1+x2)=(y1-y2)(y1+y2)又∵x1+x2=2,y1+y2=2∴2(x1-x2)=y1-y1即kAB=
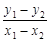 =2但渐近线斜率为±
=2但渐近线斜率为± ,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在
,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
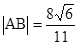 。
。 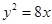 的焦点到双曲线
的焦点到双曲线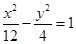 的渐近线的距离为( )
的渐近线的距离为( )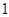
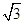
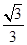
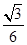
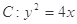 与直线
与直线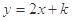 相交于
相交于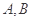 两点,且
两点,且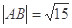
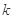 的值。
的值。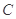 上是否存在点
上是否存在点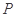 ,使得
,使得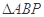 的重心恰为抛物线
的重心恰为抛物线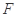 ,若存在,求点
,若存在,求点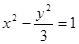 的左、右焦点,P为C上一点,若△PF1F2的面积为6,则
的左、右焦点,P为C上一点,若△PF1F2的面积为6,则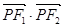 = 。
= 。 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )



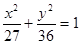 有共同焦点,并且与其中一个交点的纵坐标为4,则这个双曲线的方程为_____。
有共同焦点,并且与其中一个交点的纵坐标为4,则这个双曲线的方程为_____。 的离心率为
的离心率为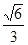 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6。
,椭圆C上任意一点到椭圆两个焦点的距离之和为6。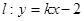 与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线
与椭圆C交于A、B两点,点P(0,1),且|PA|=|PB|,求直线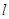 的方程。
的方程。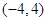 的抛物线的标准方程是
的抛物线的标准方程是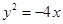
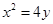
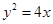 或
或