题目内容
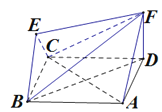
【题目】如图,在四棱锥![]() 中,底面四边形
中,底面四边形![]() 是菱形,点
是菱形,点![]() 在线段
在线段![]() 上,
上,![]() ∥平面
∥平面![]() .
.

(1)证明:点![]() 为线段
为线段![]() 中点;
中点;
(2)已知![]() 平面
平面![]() ,
,![]() ,点
,点![]() 到平面
到平面![]() 的距离为1,四棱锥
的距离为1,四棱锥![]() 的体积为
的体积为![]() ,求
,求![]() .
.
【答案】(1)见解析(2)![]()
【解析】
(1)连结![]() ,与
,与![]() 相交于点
相交于点![]() ,由线面平行的性质定理即可证得
,由线面平行的性质定理即可证得![]() ,在
,在![]() 中,由
中,由![]() 为
为![]() 中点,即可证得结论;
中点,即可证得结论;
(2)![]() 平面
平面![]() ,
,![]() ,可证得平面
,可证得平面![]() 平面
平面![]() ,由面面垂直的性质可证得
,由面面垂直的性质可证得![]() 面
面![]() ,由已知可得
,由已知可得![]() ,根据体积公式即可求得
,根据体积公式即可求得![]() .
.
解:(1)连结![]() ,与
,与![]() 相交于点
相交于点![]() ,连结
,连结![]() ,则经过
,则经过![]() 的平面
的平面![]() 与平面
与平面![]() 交线为
交线为![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
因为四边形![]() 是菱形,
是菱形,
所以![]() 为
为![]() 的中点,
的中点,
所以![]() 是
是![]() 中位线,于是
中位线,于是![]() 为线段
为线段![]() 中点.
中点.
(2)因为![]() 平面
平面![]() ,
,
所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离等于1.
的距离等于1.
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]()
![]() .因为
.因为![]() ,
,
所以![]() 面
面![]() ,因此
,因此![]() .
.
因为![]() ,所以四边形
,所以四边形![]() 是边长为2的菱形,面积为
是边长为2的菱形,面积为![]() ,
,
所以四棱锥![]() 的体积为
的体积为![]() ,
,
由![]() ,得
,得![]() .
.


练习册系列答案
相关题目
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: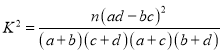 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |