题目内容
三枚硬币:第一枚的正面贴上红色标签,反面贴上蓝色;第二枚的正面贴上蓝色标签,反面贴上黄色;第三枚的正面贴上黄色标签,反面贴上红色.同时抛三枚,则三枚硬币落地后颜色各不相同的概率是
.
| 1 |
| 4 |
| 1 |
| 4 |
分析:此题需要三步完成,抛每一枚硬币为一步,每一步有两个选择,所以采用树状图可以表示出所有可能,共8种可能情况.
解答: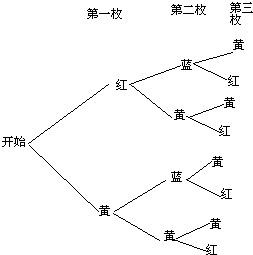 解:画树状图,
解:画树状图,
∴一共有8种情况,三枚硬币落地后颜色各不相同的有2种情况,
∴三枚硬币落地后颜色各不相同的概率是
=
.
故答案为:
.
 解:画树状图,
解:画树状图,∴一共有8种情况,三枚硬币落地后颜色各不相同的有2种情况,
∴三枚硬币落地后颜色各不相同的概率是
| 2 |
| 8 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本小题主要考查等可能事件的概率.属于基础题.此题考查的是用树状图法求概率;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.

练习册系列答案
相关题目
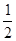 ,那么掷两次一定会出现一次正面的情况
,那么掷两次一定会出现一次正面的情况