题目内容
设函数
(1)当
 时,求f(x)的最大值.
时,求f(x)的最大值.(2)令
 ,以其图象上任一点P(x,y)为切点的切线的斜率
,以其图象上任一点P(x,y)为切点的切线的斜率 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(1)当 时,求出f(x),进而求得f′(x),由f′(x)的符号判断f(x)的单调性,根据单调性求出f(x)的最大值.
时,求出f(x),进而求得f′(x),由f′(x)的符号判断f(x)的单调性,根据单调性求出f(x)的最大值.
(2)求出 ,由题意可得
,由题意可得  在x∈(0,3]上恒成立,易知当x=1时,
在x∈(0,3]上恒成立,易知当x=1时, 取得最大值
取得最大值 ,由此求得实数a的取值范围.
,由此求得实数a的取值范围.
解答:解:(1)当 时,
时, ,
,

易知f(x)在(0,1]上递增,在[1,+∞)上递减,故f(x)的最大值为 .(6分)
.(6分)
(2) ,
, .
.
由题意 ,x∈(0,3]恒成立,即
,x∈(0,3]恒成立,即 在x∈(0,3]上恒成立.
在x∈(0,3]上恒成立.
易知当x=1时, 取得最大值
取得最大值 ,
,
故 . (12分)
. (12分)
点评:本题主要考查利用导数求曲线在某点的切线斜率,求二次函数在闭区间上的最值,利用导数求函数在闭区间上的最值,属于中档题.
 时,求出f(x),进而求得f′(x),由f′(x)的符号判断f(x)的单调性,根据单调性求出f(x)的最大值.
时,求出f(x),进而求得f′(x),由f′(x)的符号判断f(x)的单调性,根据单调性求出f(x)的最大值.(2)求出
 ,由题意可得
,由题意可得  在x∈(0,3]上恒成立,易知当x=1时,
在x∈(0,3]上恒成立,易知当x=1时, 取得最大值
取得最大值 ,由此求得实数a的取值范围.
,由此求得实数a的取值范围.解答:解:(1)当
 时,
时, ,
,
易知f(x)在(0,1]上递增,在[1,+∞)上递减,故f(x)的最大值为
 .(6分)
.(6分)(2)
 ,
, .
.由题意
 ,x∈(0,3]恒成立,即
,x∈(0,3]恒成立,即 在x∈(0,3]上恒成立.
在x∈(0,3]上恒成立.易知当x=1时,
 取得最大值
取得最大值 ,
,故
 . (12分)
. (12分)点评:本题主要考查利用导数求曲线在某点的切线斜率,求二次函数在闭区间上的最值,利用导数求函数在闭区间上的最值,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
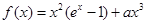
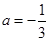 时,求
时,求 的单调区间;
的单调区间;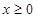 时
时 恒成立,求实数
恒成立,求实数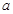 的取值范围。
的取值范围。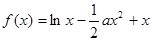
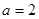 时,求
时,求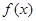 的最大值;
的最大值;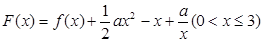 ,以其图象上任意一点
,以其图象上任意一点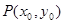 为切点的切线的斜率
为切点的切线的斜率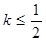 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;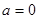 时,方程
时,方程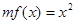 有唯一实数解,求正数
有唯一实数解,求正数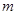 的值.
的值.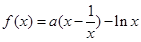
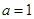 时,求曲线
时,求曲线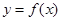 在点
在点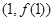 处的切线方程;
处的切线方程;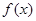 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数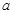 的取值范围;
的取值范围;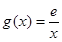 ,若在
,若在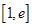 上至少存在一点
上至少存在一点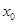 使
使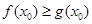 成立,求实数
成立,求实数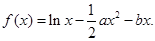
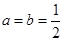 时,求
时,求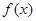 的最大值;
的最大值;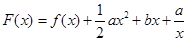 ,(
,(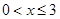 ),其图象上任意一点
),其图象上任意一点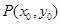 处切线的斜率
处切线的斜率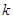 ≤
≤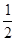 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
,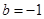 ,方程
,方程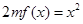 有唯一实数解,求正数
有唯一实数解,求正数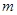 的值.
的值.