题目内容
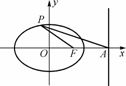
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.
(1) 求椭圆C的方程;
(2) 点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
解:(1) 设椭圆C的方程为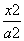 +
+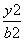 =1(a>b>0),由已知,得
=1(a>b>0),由已知,得 ∴b=
∴b= .
.
所以椭圆C的方程为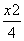 +
+  =1.
=1.
(2) 由 =e=
=e=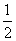 ,得PF=
,得PF=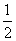 PM.∴PF≠PM.
PM.∴PF≠PM.
①若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与PM相等.
②若FM=PM,设P(x,y)(x≠±2),则M(4,y).∴ =4-x,∴9+y2=16-8x+x2.又由
=4-x,∴9+y2=16-8x+x2.又由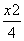 +
+ =1,得y2=3-
=1,得y2=3- x2.∴9+3-
x2.∴9+3- x2=16-8x+x2,
x2=16-8x+x2,
∴ x2-8x+4=0.∴7x2-32x+16=0.∴x=
x2-8x+4=0.∴7x2-32x+16=0.∴x= 或x=4.
或x=4.
∵x∈(-2,2),∴x= .∴P
.∴P .综上,存在点P
.综上,存在点P ,使得△PFM为等腰三角形.
,使得△PFM为等腰三角形.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 =
= ,则sinθ+cosθ=________.
,则sinθ+cosθ=________.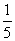 .
. ,N={α|-π<α<π},则M∩N=________.
,N={α|-π<α<π},则M∩N=________.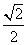 的直线l与椭圆
的直线l与椭圆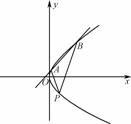
 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,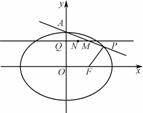
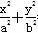 =1(a>b>0)的右焦点F,其右准线与x轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是________.
=1(a>b>0)的右焦点F,其右准线与x轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是________.