题目内容
(本题满分12分)已知方程 表示一个圆.
表示一个圆.
(1)求实数 的取值范围;
的取值范围;
(2)求圆心 的轨迹方程.
的轨迹方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)

解析试题分析:(1)方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件是A=C≠0,B=0,且D2+E2-4F>0,代入公式即可解出取值范围;(2)设出圆心 由题意可得
由题意可得 , 消参数
, 消参数 ,此时注意参数取值范围为
,此时注意参数取值范围为 ,所以轨迹方程为
,所以轨迹方程为

试题解析:(1) ,
,
解得: .5分
.5分
(2)设圆心
则 , 消参数
, 消参数 得:
得: 7分
7分
由(1) 得
得 9分
9分
所以圆心C的轨迹方程为:
 12分
12分
考点:圆的方程、轨迹方程.

练习册系列答案
相关题目
已知直线 与直线
与直线 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
| A.1 | B.2 | C. | D.4 |
若函数 的图象在点
的图象在点 处的切线
处的切线 被圆
被圆 所截得的弦长是
所截得的弦长是 ,则
,则
A. | B. | C. | D. |
已知直线 与圆
与圆 有公共点, 且公共点的横坐标和纵坐标均为整数,
有公共点, 且公共点的横坐标和纵坐标均为整数,
那么这样的直线共有 ( )
| A.60条 | B.66条 | C.70条 | D.71条 |
已知过曲线 上一点P,原点为O,直线PO的倾斜角为
上一点P,原点为O,直线PO的倾斜角为 ,则P点坐标是( )
,则P点坐标是( )
| A.(3,4) | B. | C.(-3,-4) | D. |
如果输入 ,那么执行下图中算法后的输出结果是( )
,那么执行下图中算法后的输出结果是( )
A. | B. | C. | D. |
 与
与 的夹角为
的夹角为 ,若(
,若( )
) (
( ),则
),则 .
. ,沿着较短的对角线
,沿着较短的对角线 对折,使得
对折,使得 ,
,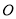 为
为 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足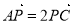 。
。
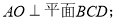
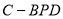 的体积;
的体积; 的余弦值.
的余弦值. =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,过点
,过点 和
和 的直线与坐标原点距离为
的直线与坐标原点距离为 .
. ,若直线
,若直线 与椭圆相交于
与椭圆相交于 两点,试判断是否存在
两点,试判断是否存在 值,使以
值,使以 为直径的圆过定点
为直径的圆过定点 ?若存在求出这个
?若存在求出这个