题目内容
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,
∠BCF=![]() ,AD=
,AD=![]() ,EF=2.(Ⅰ)求证: AE∥平面DCF;
,EF=2.(Ⅰ)求证: AE∥平面DCF;
(Ⅱ)设![]() ,当
,当![]() 取何值时,二面角A—EF—C的大小为
取何值时,二面角A—EF—C的大小为![]() ?
?
(Ⅰ) 见解析 (Ⅱ) ![]()
解析:
(I)解法一:∵ 四边形ABCD是矩形,
∴AB∥DC . ……………… 1分
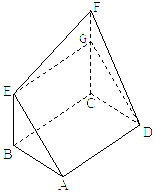 又∵ BE∥CF , AB∩BE=B,
又∵ BE∥CF , AB∩BE=B,
∴平面ABE∥平面DCF . ………… 3分
又AE![]() 平面ABE,
平面ABE,
∴AE∥平面DCF . ……… 5分
解法二:过E作EG∥BC交FC于G,连结DG , ………1分
∵BE∥CF ,
∴四边形BCGE是平行四边形 ,
∴EG∥BC∥AD,且EG=BC=AD,
∴四边形ADGE也是平行四边形 , ………3分
∴AE∥DG .又AE![]() 平面DCF,DG
平面DCF,DG![]() 平面DCF ,
平面DCF ,
∴AE∥平面 DCF . ………5分
(II)解法一: 过E作GE⊥CF交CF于G,
由已知 EG∥BC∥AD,且EG=BC=AD,
∴EG=AD=![]() ,又EF=2, ∴GF=1 . ………………6分
,又EF=2, ∴GF=1 . ………………6分
∵四边形ABCD是矩形, ∴DC⊥BC .
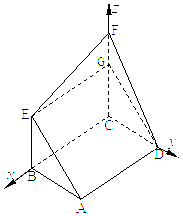 ∵∠BCF=
∵∠BCF=![]() , ∴FC⊥BC,
, ∴FC⊥BC,
又平面AC⊥平面BF,平面AC∩平面BF=BC,
∴FC⊥平面AC , ∴FC⊥CD . …………7分
分别以CB、CD、CF为轴建立空间直角坐标系.
设BE=m,由![]() ,得AB=
,得AB=![]() m .
m .
∴ A(![]() ,
,![]() m,0),E(
m,0),E(![]() ,0,m),F(0,0,m+1),
,0,m),F(0,0,m+1),
∴![]() =(0,-
=(0,-![]() m ,m),
m ,m),![]() =(-
=(-![]() ,0,1). …………8分
,0,1). …………8分
设平面AEF的法向量![]() =(x,y,z),
=(x,y,z),
由![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,得
=0,得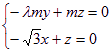 ,∴
,∴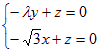 ,
,
令![]() =
=![]() ,可得平面AEF的一个法向量
,可得平面AEF的一个法向量![]() =(
=( ![]() ,
,![]() ,
,![]()
![]() ). ………10分
). ………10分
又![]() =(0,
=(0,![]() m,0)是平面CEF的一个法向量,
m,0)是平面CEF的一个法向量,
∴ 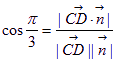 ,即
,即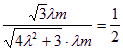 , 解得
, 解得![]() =
=![]() .
.
∴当![]() 的值为
的值为![]() 时,二面角A—EF—C的大小为
时,二面角A—EF—C的大小为![]() . ………………13分
. ………………13分
解法二:过E作GE⊥CF交CF于G,
由已知EG∥BC∥AD,且EG=BC=AD,
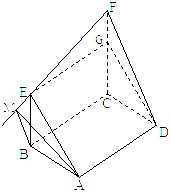 ∴EG=
∴EG=![]() ,又EF=2, ∴sin∠EFG=
,又EF=2, ∴sin∠EFG=![]() . ……………6分
. ……………6分
∵四边形ABCD是矩形, ∴AB⊥BC
又平面AC⊥平面BF,平面AC∩平面BF=BC,
∴AB⊥平面BF .
过B作BM⊥FE交EF于M,连结AM,
则∠AMB为二面角A—EF—C的平面角, ……… 8分
∴∠AMB=![]() .
.
由已知 ![]() ,设BE=m,则AB=
,设BE=m,则AB=![]() m ,
m ,
∴BM= BE·sin∠MEB =BE·sin∠EFG= ![]() m . ………………10分
m . ………………10分
在Rt△ABM中,tan![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴ ![]() =
=![]() .
.
∴当![]() 的值取
的值取![]() 时,二面角A—EF—C的大小为
时,二面角A—EF—C的大小为![]() . ………………13分
. ………………13分

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案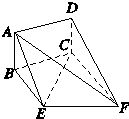 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF= 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°, 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD= 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=