题目内容
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比 =x,求公园ABCD所占面积S关于x的函数解析式.
=x,求公园ABCD所占面积S关于x的函数解析式.
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽应如何设计?

(1)设休闲区的宽为a米,则其长为ax米,由a2x=4000,得a= .
.
则S=(a+8)(ax+20)=a2x+(8x+20)a+160
=4000+(8x+20)· +160
+160
=80 +4160(x>1).
+4160(x>1).
(2)S≥80 ×2
×2 +4160=1600+4160=5760.当且仅当2
+4160=1600+4160=5760.当且仅当2 =
= ,即x=2.5时取等号,此时a=40, ax=100.所以要使公园所占面积最小,休闲区A1B1C1D1应设计为长100米,宽40米.
,即x=2.5时取等号,此时a=40, ax=100.所以要使公园所占面积最小,休闲区A1B1C1D1应设计为长100米,宽40米.

练习册系列答案
相关题目
 的值.
的值. ,则它的表面积等于 .
,则它的表面积等于 .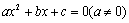 有有理根,那么
有有理根,那么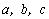 中至少有一个是偶数时,下列假设中正确的是( )
中至少有一个是偶数时,下列假设中正确的是( ) ,则z的共轭复数为( )
,则z的共轭复数为( ) 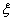 服从分布B(n,p),且E(
服从分布B(n,p),且E(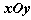 中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.
中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.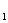 :
: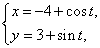 (t为参数), C
(t为参数), C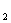 :
: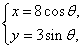 (
(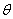 为参数)。
为参数)。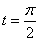 ,Q为C
,Q为C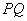 中点
中点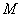 到直线
到直线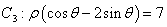 距离的最小值.
距离的最小值.