题目内容
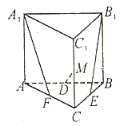
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
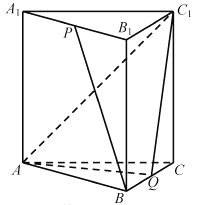
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
【答案】(1)![]()
(2)![]()
【解析】分析:(1)先建立空间直角坐标系,设立各点坐标,根据向量数量积求得向量![]() 的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面
的夹角,再根据向量夹角与异面直线所成角的关系得结果;(2)利用平面的方向量的求法列方程组解得平面![]() 的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
的一个法向量,再根据向量数量积得向量夹角,最后根据线面角与所求向量夹角之间的关系得结果.
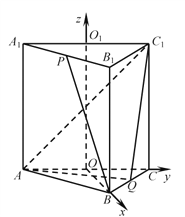
详解:如图,在正三棱柱ABCA1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,OO1⊥OB,以![]() 为基底,建立空间直角坐标系Oxyz.
为基底,建立空间直角坐标系Oxyz.
因为AB=AA1=2,
所以![]() .
.
(1)因为P为A1B1的中点,所以![]() ,
,
从而![]() ,
,
故 .
.
因此,异面直线BP与AC1所成角的余弦值为![]() .
.
(2)因为Q为BC的中点,所以![]() ,
,
因此![]() ,
,![]() .
.
设n=(x,y,z)为平面AQC1的一个法向量,
则 即
即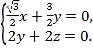
不妨取![]() ,
,
设直线CC1与平面AQC1所成角为![]() ,
,
则 ,
,
所以直线CC1与平面AQC1所成角的正弦值为![]() .
.

【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: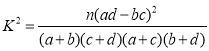 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |