题目内容
已知椭圆G: 的离心率为
的离心率为 ,且右顶点为A(2,0).
,且右顶点为A(2,0).(Ⅰ)求椭圆G的方程;
(Ⅱ)过点P(0,2)的直线l与椭圆G交于A,B两点,当以线段AB为直径的圆经过坐标原点时,求直线l的方程.
【答案】分析:(Ⅰ)由椭圆C的离心率e= =
= ,右顶点为A(2,0),能求出椭圆的方程.
,右顶点为A(2,0),能求出椭圆的方程.
(Ⅱ)设直线l的方程为y=kx=2.由方程组 ,得(4k2+1)x2+16kx+12=0.由方程有两个不等的实数根,解得|k|>
,得(4k2+1)x2+16kx+12=0.由方程有两个不等的实数根,解得|k|> .设A(x1,y1),B(x2,y2),则x1+x2=
.设A(x1,y1),B(x2,y2),则x1+x2= ,x1x2=
,x1x2= .因为以线段AB为直径的圆经过坐标原点,所以x1x2+y1y2=0,由此能够求出直线l的方程.
.因为以线段AB为直径的圆经过坐标原点,所以x1x2+y1y2=0,由此能够求出直线l的方程.
解答:解:(Ⅰ)∵椭圆C的离心率e= =
= ,右顶点为A(2,0),
,右顶点为A(2,0),
∴a=2,c= ,b=1.
,b=1.
所以椭圆的方程为 .…(4分)
.…(4分)
(Ⅱ)设直线l的方程为y=kx=2.
由方程组 ,得(4k2+1)x2+16kx+12=0.①…(6分)
,得(4k2+1)x2+16kx+12=0.①…(6分)
因为方程①有两个不等的实数根,
所以△=(16k)2-4(4k2+1)×12>0,
解得|k|> .…(7分)
.…(7分)
设A(x1,y1),B(x2,y2),则x1+x2= ,x1x2=
,x1x2= .②
.②
因为以线段AB为直径的圆经过坐标原点,
所以 ,
, =0,即有x1x2+y1y2=0.…(9分)
=0,即有x1x2+y1y2=0.…(9分)
所以x1x2+(kx1+2)(kx2+2)=0,
所以(k2+1)x1x2+2k(x1+x2)+4=0.③
将②代入③得 ,
,
所以12(k2+1)-2×16k2+4(4k2+1)=0,
解得k=±2.…(13分)
满足|k|> ,
,
所求直线l的方程为y=±2x+2.…(14分)
点评:本题考查椭圆方程的求法和直线方程的求法,综合性强,难度大.解题时要认真审题,仔细解答,注意解题能力的培养.
 =
= ,右顶点为A(2,0),能求出椭圆的方程.
,右顶点为A(2,0),能求出椭圆的方程.(Ⅱ)设直线l的方程为y=kx=2.由方程组
 ,得(4k2+1)x2+16kx+12=0.由方程有两个不等的实数根,解得|k|>
,得(4k2+1)x2+16kx+12=0.由方程有两个不等的实数根,解得|k|> .设A(x1,y1),B(x2,y2),则x1+x2=
.设A(x1,y1),B(x2,y2),则x1+x2= ,x1x2=
,x1x2= .因为以线段AB为直径的圆经过坐标原点,所以x1x2+y1y2=0,由此能够求出直线l的方程.
.因为以线段AB为直径的圆经过坐标原点,所以x1x2+y1y2=0,由此能够求出直线l的方程.解答:解:(Ⅰ)∵椭圆C的离心率e=
 =
= ,右顶点为A(2,0),
,右顶点为A(2,0),∴a=2,c=
 ,b=1.
,b=1.所以椭圆的方程为
 .…(4分)
.…(4分)(Ⅱ)设直线l的方程为y=kx=2.
由方程组
 ,得(4k2+1)x2+16kx+12=0.①…(6分)
,得(4k2+1)x2+16kx+12=0.①…(6分)因为方程①有两个不等的实数根,
所以△=(16k)2-4(4k2+1)×12>0,
解得|k|>
 .…(7分)
.…(7分)设A(x1,y1),B(x2,y2),则x1+x2=
 ,x1x2=
,x1x2= .②
.②因为以线段AB为直径的圆经过坐标原点,
所以
 ,
, =0,即有x1x2+y1y2=0.…(9分)
=0,即有x1x2+y1y2=0.…(9分)所以x1x2+(kx1+2)(kx2+2)=0,
所以(k2+1)x1x2+2k(x1+x2)+4=0.③
将②代入③得
 ,
,所以12(k2+1)-2×16k2+4(4k2+1)=0,
解得k=±2.…(13分)
满足|k|>
 ,
,所求直线l的方程为y=±2x+2.…(14分)
点评:本题考查椭圆方程的求法和直线方程的求法,综合性强,难度大.解题时要认真审题,仔细解答,注意解题能力的培养.

练习册系列答案
相关题目

 的离心率为
的离心率为 ,右焦点为
,右焦点为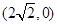 ,斜率为1的直线
,斜率为1的直线 与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)
与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)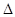 PAB的面积
PAB的面积 的离心率为
的离心率为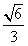 ,右焦点为(2
,右焦点为(2 ,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。
,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( ) 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( ) 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )