题目内容
(本题13分)
已知椭圆G:
 的离心率为
的离心率为 ,右焦点为
,右焦点为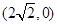 ,斜率为1的直线
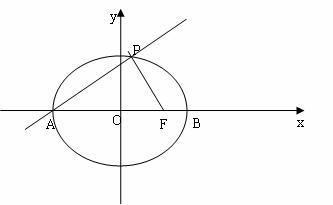
,斜率为1的直线 与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)
与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)
(1) 求椭圆G的方程
(2)
求 PAB的面积
PAB的面积
【答案】
解:(Ⅰ)由已知得
解得
又
所以椭圆G的方程为
(Ⅱ)设直线l的方程为
由 得
得
设A、B的坐标分别为 AB中点为E
AB中点为E ,
,
则

因为AB是等腰△PAB的底边,所以PE⊥AB.
所以PE的斜率 解得m=2。
解得m=2。
此时方程①为 解得
解得
所以 所以|AB|=
所以|AB|= .
.
此时,点P(—3,2)到直线AB: 的距离
的距离
所以△PAB的面积S=
【解析】略

练习册系列答案
相关题目
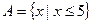 ,
,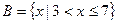 ,
,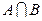 ;(2)
;(2)
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 ;
; ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1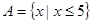 ,
,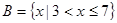 ,
,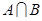 ;(2)
;(2)