题目内容
已知椭圆G: 的离心率为
的离心率为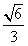 ,右焦点为(2
,右焦点为(2 ,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。
,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。
(Ⅰ)求椭圆G的方程;
(Ⅱ)求△PAB的面积。
 的离心率为
的离心率为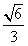 ,右焦点为(2
,右焦点为(2 ,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。
,0)。斜率为1的直线l与椭圆G交于A,B两点,以AB为底边作等腰三角形,顶点为P(-3,2)。(Ⅰ)求椭圆G的方程;
(Ⅱ)求△PAB的面积。
解:(Ⅰ)由已知得 ,解得
,解得 ,
,
又 ,
,
所以椭圆G的方程为 。
。
(Ⅱ)设直线l的方程为y=x+m,
由 得
得 ,①
,①
设A、B的坐标分别为 ,AB中点为E
,AB中点为E ,
,
则 ,
,
因为AB是等腰△PAB的底边,所以PE⊥AB,
所以PE的斜率 ,解得m=2。
,解得m=2。
此时方程①为 ,解得
,解得 ,
,
所以 ,
,
所以|AB|= ,
,
此时,点P(-3,2)到直线AB:x-y+2=0的距离 ,
,
所以△PAB的面积S= 。
。
 ,解得
,解得 ,
,又
 ,
,所以椭圆G的方程为
 。
。(Ⅱ)设直线l的方程为y=x+m,
由
 得
得 ,①
,①设A、B的坐标分别为
 ,AB中点为E
,AB中点为E ,
,则
 ,
,因为AB是等腰△PAB的底边,所以PE⊥AB,
所以PE的斜率
 ,解得m=2。
,解得m=2。此时方程①为
 ,解得
,解得 ,
,所以
 ,
,所以|AB|=
 ,
,此时,点P(-3,2)到直线AB:x-y+2=0的距离
 ,
,所以△PAB的面积S=
 。
。 
练习册系列答案
相关题目

 的离心率为
的离心率为 ,右焦点为
,右焦点为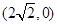 ,斜率为1的直线
,斜率为1的直线 与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)
与椭圆G交于A,B两点,以AB为底的等腰三角形顶点为P(-3,2)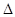 PAB的面积
PAB的面积 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( ) 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( ) 的离心率为
的离心率为 ,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )
,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是( )