题目内容
若△ABC的三个内角满足:2B=A+C,且A<B<C,tanAtanC=2+
,求A,B,C的大小.
| 3 |
考点:两角和与差的正切函数
专题:解三角形
分析:由A,B及C成等差数列,利用等差数列的性质得到A+C=2B,再利用三角形的内角和定理求出B的度数,进而得到A+C的度数,利用两角和与差的正切函数公式化简tan(A+C),根据A+C的度数,利用特殊角的三角函数值求出tan(A+C)的值,把已知的tanAtanC的值代入,求出tanA+tanC的值,根据韦达定理得到关于tanA和tanC的方程,求出方程的解得到tanA和tanC的值,利用特殊角的三角函数值求出A和C的度数.
解答:
解:由A+B+C=180°及A+C=2B,
得B=60°,A+C=120°,
∴tan(A+C)=
=-
,又tanAtanC=2+
,
∴tanA+tanC=3+
,
∴tanA,tanC为二次方程x2-(3+
)x+2+
=0的根,
∴tanA=1,tanA=2+
或tanC=2+
,tanC=1,
∵A<B<C,
∴A=45°,C=75°.B=60°.
得B=60°,A+C=120°,
∴tan(A+C)=
| tanA+tanC |
| 1-tanAtanC |
| 3 |
| 3 |
∴tanA+tanC=3+
| 3 |
∴tanA,tanC为二次方程x2-(3+
| 3 |
| 3 |
∴tanA=1,tanA=2+
| 3 |
| 3 |
∵A<B<C,
∴A=45°,C=75°.B=60°.
点评:此题属于解三角形的题型,涉及的知识有:两角和与差的正切函数公式,等差数列的性质,韦达定理,正弦定理以及特殊角的三角函数值,注意不要错解.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知α,β∈[-
,
],且αsinα-βsinβ>0,则下列结论正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、α3>β3 |
| B、α+β>0 |
| C、|α|<|β| |
| D、|α|>|β| |
下列函数中,在定义域内是减函数的为( )
| A、y=-3x2 | ||
B、y=-
| ||
| C、y=5x | ||
| D、y=-4x |
对于非空数集A,若实数M满足对任意的a∈A恒有a≤M,则M为A的上界;若A的所有上界中存在最小值,则称此最小值为A的上确界,那么下列函数的值域中具有上确界的是( )
A、y=
| ||||
B、y=(-
| ||||
C、y=
| ||||
| D、y=lnx |
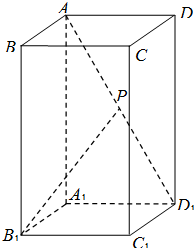 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).