题目内容
正数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,
,![]() 。
。
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个单调递增数列,求
是一个单调递增数列,求![]() 的取值范围;
的取值范围;
(3)若![]() 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数![]() 。
。
(1)证明:![]() ①
①
![]() ②
②
②-①:![]() ③
③
任意![]() ,
,![]() ∴
∴![]()
(2)解:计算![]() ,∴
,∴![]()
根据数列是隔项成等差,写出数列的前几项:
![]()
所以奇数项是递增数列,偶数项是递增数列,整个数列成单调递增的充要条件是
![]() 解得
解得![]()
(3)解:![]()
![]()
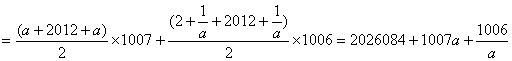
![]() 是一个整数,所以
是一个整数,所以![]() 一共4个 对一个得1分,合计4分
一共4个 对一个得1分,合计4分
另解:
![]()
![]()

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 ,求
,求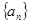 的前
的前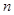 项和
项和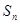 满足:
满足: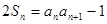 ,
,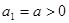
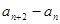 是一个定值;
是一个定值;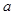 的取值范围;
的取值范围; 是一个整数,求符合条件的自然数
是一个整数,求符合条件的自然数 的前
的前 项和
项和 满足:
满足: ,
, 常数
常数
 是一个定值;
是一个定值;