题目内容
(理)正数列 的前
的前 项和
项和 满足:
满足: ,
, 常数
常数
(1)求证: 是一个定值;
是一个定值;
(2)若数列 是一个周期数列,求该数列的周期;
是一个周期数列,求该数列的周期;
(3)若数列 是一个有理数等差数列,求
是一个有理数等差数列,求 .
.
(理)证明:(1)
 (1)
(1)
 (2)
(2)
 :
:  (3)
(3)

 (4)
(4)
……………4分
(2)计算
 ……………6分
……………6分
根据数列是隔项成等差,写出数列的前几项:
 ,
, ,
, ,
, ,
, ,。。。。
,。。。。
当 时,奇数项和偶数项都是单调递增的,所以不可能是周期数列
……………8分
时,奇数项和偶数项都是单调递增的,所以不可能是周期数列
……………8分
所以 时,数列写出数列的前几项:
时,数列写出数列的前几项:
 ,
,
 ,
,
 ,
,
 ,,。。。。
,,。。。。
所以当 且
且 时,该数列的周期是2,
……………9分
时,该数列的周期是2,
……………9分
当 时,该数列的周期是1,
……………10分
时,该数列的周期是1,
……………10分
(3)因为数列 是一个有理等差数列,所以
是一个有理等差数列,所以
化简 ,
,
 是有理数
……………12分
是有理数
……………12分
设 ,是一个完全平方数,设为
,是一个完全平方数,设为 ,
, 均是非负整数
均是非负整数
 时,
时, ……………14分
……………14分
 时
时 =
= 可以分解成8组,其中
可以分解成8组,其中
只有 符合要求,
……………16分
符合要求,
……………16分
此时
 ……………18分
……………18分
或者 ,
……………12分
,
……………12分
等差数列的前几项:
 ,
, ,
, ,。。。。
,。。。。
 ……………14分
……………14分
因为数列 是一个有理等差数列
是一个有理等差数列
 是一个自然数,
是一个自然数, ……………16分
……………16分
此时
 ……………18分
……………18分
如果没有理由,猜想: ,解答
,解答
 得2分
得2分

 得2分
得2分
【解析】略

 的公差是
的公差是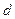 ,
, 是该数列的前
是该数列的前 项和.
项和. 表示
表示 ,其中
,其中 、
、
 ,求
,求 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 项和
项和 ,前
,前 项和
项和 ,求数列
,求数列 .”
.”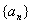 的首项
的首项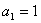 ,前
,前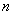 项和为
项和为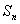 (
(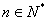 ),且点
),且点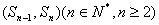 在直线
在直线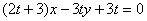 上(
上(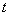 为与
为与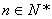 )为等比数列;
)为等比数列;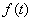 ,数列
,数列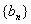 满足
满足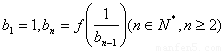 ,设
,设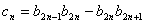 ,求数列
,求数列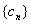 的前
的前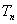 ;
;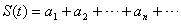 ,求函数
,求函数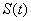 的值域.
的值域.