题目内容
已知直角坐标系中圆C方程为F(x,y)=0,P(x0,y0)为圆内一点(非圆心),那么方程F(x,y)=F(x0,y0)所表示的曲线是( )
分析:设圆C方程,确定圆心坐标与半径,求出F(x,y)-F(x0,y0)=0的表达式,即可得到结论.
解答:解:设圆C方程为F(x,y)=x2+y2+Dx+Ey+F=0,圆的圆心坐标为(-
,-
),圆的半径为
∵P(x0,y0)为圆内一点,
∴F(x0,y0)<0,即x02+y02+Dx0+Ey0+F<0,
∴x2+y2+Dx+Ey+F-(x02+y02+Dx0+Ey0+F)=0
令F′=-(x02+y02+Dx0+Ey0),则F′>F
∴F(x,y)-F(x0,y0)=0表示圆,圆的圆心坐标为(-
,-
),圆的半径为
且
<
∴方程F(x,y)=F(x0,y0)所表示的曲线是比圆C半径小,与圆C同心的圆
故选B.
| D |
| 2 |
| E |
| 2 |
| ||
| 2 |
∵P(x0,y0)为圆内一点,
∴F(x0,y0)<0,即x02+y02+Dx0+Ey0+F<0,
∴x2+y2+Dx+Ey+F-(x02+y02+Dx0+Ey0+F)=0
令F′=-(x02+y02+Dx0+Ey0),则F′>F
∴F(x,y)-F(x0,y0)=0表示圆,圆的圆心坐标为(-
| D |
| 2 |
| E |
| 2 |
| ||
| 2 |
且
| ||
| 2 |
| ||
| 2 |
∴方程F(x,y)=F(x0,y0)所表示的曲线是比圆C半径小,与圆C同心的圆
故选B.
点评:本题考查圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 方程为
方程为 ,
, 为圆内一点(非圆心),
为圆内一点(非圆心), 所表示的曲线是———————— ( )
所表示的曲线是———————— ( )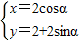 (α为参数),若以原点O为极点,以x轴正半轴为极轴建立极坐标系,则圆C的极坐标方程为 .
(α为参数),若以原点O为极点,以x轴正半轴为极轴建立极坐标系,则圆C的极坐标方程为 .