题目内容
在梯形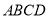 中,
中, ,
,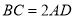 ,
,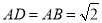 ,
,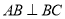 ,如图把
,如图把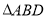 沿
沿 翻折,使得平面
翻折,使得平面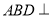 平面
平面 .
.
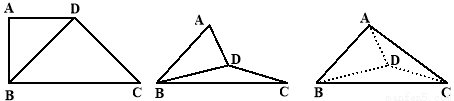
(Ⅰ)求证: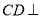 平面
平面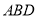 ;
;
(Ⅱ)若点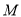 为线段
为线段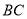 中点,求点
中点,求点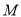 到平面
到平面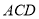 的距离.
的距离.
(Ⅰ) 见解析;(Ⅱ) 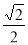
【解析】
试题分析:(Ⅰ)证明线面垂直,利用判定定理知转化为证明线线垂直,本题中因为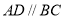 ,
,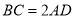 ,
,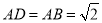 ,
,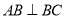 ,所以
,所以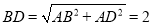 ,
,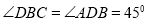 ,
,
 ,
,
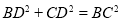 ,所以
,所以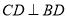 .因为平面
.因为平面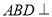 平面
平面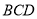 ,平面
,平面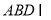 平面
平面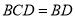 ,
,
所以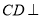 平面
平面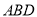 ;(Ⅱ)通过建立坐标系,利用公式
;(Ⅱ)通过建立坐标系,利用公式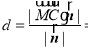 即可解决
即可解决
试题解析:(Ⅰ)证明:因为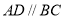 ,
,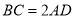 ,
,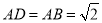 ,
,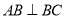 ,
,
所以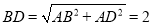 ,
,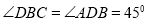
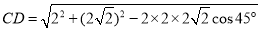
 ,
,
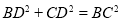 ,所以
,所以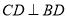 .
.
因为平面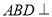 平面
平面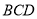 ,平面
,平面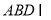 平面
平面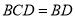 ,
,
所以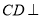 平面
平面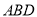 . 6分
. 6分
(Ⅱ)【解析】
由(Ⅰ)知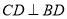 .
.
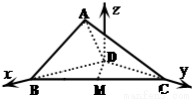
以点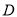 为原点,
为原点,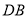 所在的直线为
所在的直线为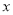 轴,
轴,
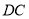 所在直线为
所在直线为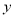 轴,
轴,
如图建立空间直角坐标系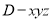 .
.
则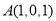 ,
,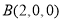 ,
,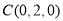 ,
,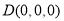 ,
,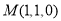 .
.
所以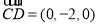 ,
, ,
,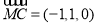 .
.
设平面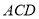 的法向量为
的法向量为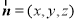 ,则
,则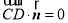 且
且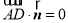 ,
,
所以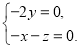 令
令 ,得平面
,得平面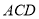 的一个法向量为
的一个法向量为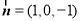
所以点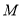 到平面
到平面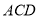 的距离为
的距离为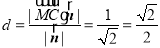 . 12分
. 12分
考点:立体几何的综合应用
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
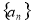 中,
中,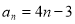 ,则首项
,则首项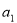 和公差
和公差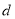 的值分别为( )
的值分别为( ) 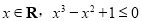 ”的否定是( )
”的否定是( )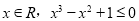

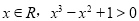

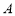 ,
,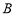 ,线段
,线段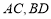 分别在这个二面角的两个面内,并且都垂直于棱
分别在这个二面角的两个面内,并且都垂直于棱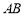 ,
,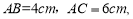
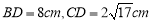 ,则这个二面角的度数为( )
,则这个二面角的度数为( )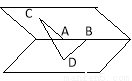
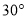 B.
B.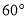 C.
C.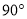 D.
D.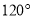
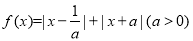 .证明:
.证明: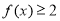 ;
;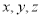 满足
满足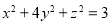 ,求证:
,求证: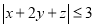
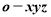 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以
中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以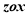 平面为投影面,则得到主视图可以为( )
平面为投影面,则得到主视图可以为( )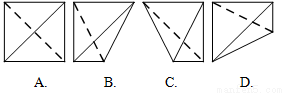
 的最小值为 .
的最小值为 .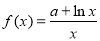 在点
在点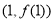 处的切线与x轴平行.
处的切线与x轴平行.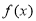 的极值;
的极值;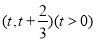 ,使函数
,使函数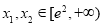 ,有
,有 ,求实数k的取值范围.
,求实数k的取值范围.