题目内容
已知函数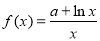 在点
在点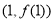 处的切线与x轴平行.
处的切线与x轴平行.
(1)求实数a的值及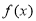 的极值;
的极值;
(2)是否存在区间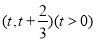 ,使函数
,使函数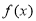 在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
(3)如果对任意的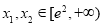 ,有
,有 ,求实数k的取值范围.
,求实数k的取值范围.
(1)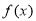 的极大值1,无极小值(2)
的极大值1,无极小值(2)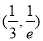 ,(3)
,(3)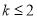
【解析】
试题分析:(1)由函数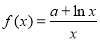 在点
在点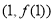 处的切线与x轴平行,对函数求导并由
处的切线与x轴平行,对函数求导并由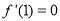 .即可求出a的值,再根据导函数的正负及可求得函数的单调性,从而可得函数的极值的情况.
.即可求出a的值,再根据导函数的正负及可求得函数的单调性,从而可得函数的极值的情况.
(2)由(1)得函数图象的走向可得,以及函数的取值范围,存在符合条件的区间,通过解不等式组即可得结论.
(3)由f(x)在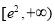 上是递减,所以不妨假设
上是递减,所以不妨假设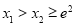 ,由此需证
,由此需证 的问题可转化,从而将问题转化为证明一个新的函数的单调性.再通过函数求导,根据k的取值需要的函数的单调区间,即可得结论.
的问题可转化,从而将问题转化为证明一个新的函数的单调性.再通过函数求导,根据k的取值需要的函数的单调区间,即可得结论.
试题解析: (1)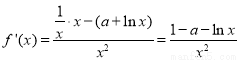
∵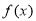 在点(1,
在点(1,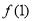 )处的切线与x轴平行∴
)处的切线与x轴平行∴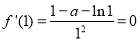
∴a=1 ∴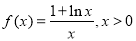
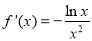 ,
,
当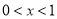 时,
时,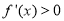 ,当
,当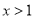 时
时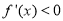 ,
,
∴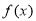 在(0,1)上单调递增,在
在(0,1)上单调递增,在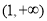 单调递减,
单调递减,
故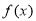 在x=1处取得极大值1,无极小值
在x=1处取得极大值1,无极小值
(2)∵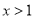 时,
时,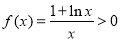 ,
,
当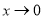 时,
时,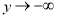 ,由(1)得
,由(1)得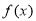 在(0,1)上单调递增,∴由零点存在原理,
在(0,1)上单调递增,∴由零点存在原理,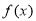 在区间(0,1)存在唯一零点,
在区间(0,1)存在唯一零点,
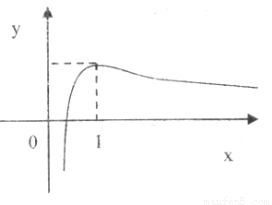
函数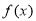 的图象如图所示
的图象如图所示
∵函数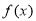 在区间
在区间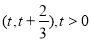 上存在极值和零点
上存在极值和零点
∴

∴存在符号条件的区间,实数t的取值范围为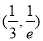 ,
,
(3)由(1)的结论知,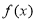 在
在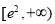 上单调递减,不妨设
上单调递减,不妨设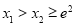 ,则,
,则,
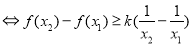
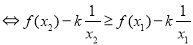
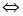 函数
函数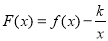 在
在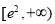 上单调递减,
上单调递减,
又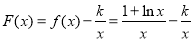 ,
,
∴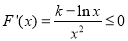 ,在
,在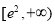 上恒成立,∴
上恒成立,∴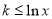 在
在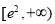 上恒成立.
上恒成立.
在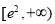 上
上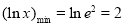 ,∴
,∴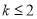
考点:1.导数.2.函数的极值.3.恒成立问题.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
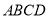 中,
中, ,
,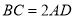 ,
,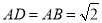 ,
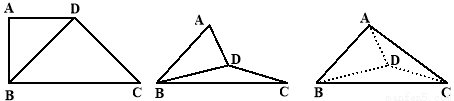
,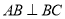 ,如图把
,如图把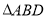 沿
沿 翻折,使得平面
翻折,使得平面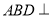 平面
平面 .
.
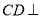 平面
平面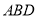 ;
;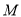 为线段
为线段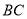 中点,求点
中点,求点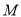 到平面
到平面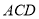 的距离.
的距离. ,
, 对应的向量分别是
对应的向量分别是 ,
, ,则复数
,则复数 对应的点位于( )
对应的点位于( )
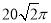 B.
B.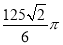 C.
C.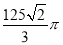 D.
D.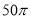
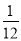 B.
B.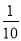 C.
C.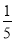 D.
D.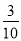
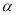 ,使
,使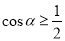 ;
;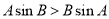 ,则B>A;
,则B>A;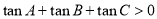 ;
;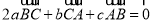 ,则△ABC的最小角小于
,则△ABC的最小角小于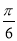 ;
; ,表示的平面区域为M,若直线
,表示的平面区域为M,若直线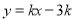 与平面区域M有公共点,则k的取值范围是( )
与平面区域M有公共点,则k的取值范围是( )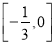 B.
B. 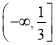 C.
C. 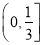 D.
D. 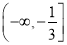
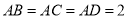 ,则平面BCD被球所截面图形的面积为 .
,则平面BCD被球所截面图形的面积为 .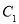 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线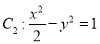 的顶点,直线
的顶点,直线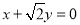 与椭圆
与椭圆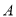 ,
,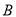 两点,且点
两点,且点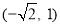 ,点
,点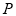 是椭圆
是椭圆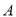 ,
,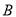 的任意一点,点
的任意一点,点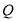 满足
满足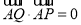 ,
,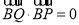 ,且
,且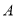 ,
,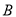 ,
,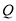 三点不共线.
三点不共线.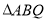 面积的最大值及此时点
面积的最大值及此时点