题目内容
(本题满分10分)选修4—5: 不等式选讲.
(Ⅰ)设函数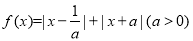 .证明:
.证明: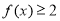 ;
;
(Ⅱ)若实数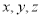 满足
满足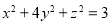 ,求证:
,求证: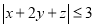
(Ⅰ) 见解析;(Ⅱ) 见解析
【解析】
试题分析:(Ⅰ)由 ,及均值不等式有
,及均值不等式有 ,所以
,所以 ;(Ⅱ)
;(Ⅱ) ,由柯西不等式得:
,由柯西不等式得:
(当且仅当 即
即 时取“
时取“ ”号)整理得:
”号)整理得: ,即
,即
试题解析: (Ⅰ)由 ,
,
有
所以 5分
5分
(Ⅱ) ,由柯西不等式得:
,由柯西不等式得:

(当且仅当 即
即 时取“
时取“ ”号)
”号)
整理得: ,即
,即 10分
10分
考点:不等式证明
考点分析: 考点1:不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ”的否定是( )
”的否定是( )



 与
与 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
 有两个零点,则
有两个零点,则 应满足的充要条件是 .
应满足的充要条件是 . , 则命题甲:
, 则命题甲: 是
是 与
与 的等差中项,命题乙:动点
的等差中项,命题乙:动点 的轨迹是椭圆,则甲是乙的 ( ).
的轨迹是椭圆,则甲是乙的 ( ).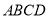 中,
中, ,
,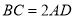 ,
,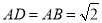 ,
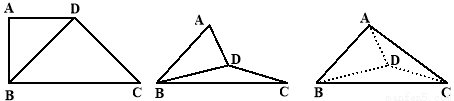
,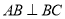 ,如图把
,如图把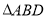 沿
沿 翻折,使得平面
翻折,使得平面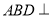 平面
平面 .
.
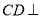 平面
平面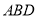 ;
;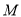 为线段
为线段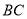 中点,求点
中点,求点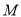 到平面
到平面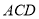 的距离.
的距离. ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
, ,
, ,若直线
,若直线
 与函数
与函数 的图象恰有两个不同的交点,则
的图象恰有两个不同的交点,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
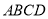 中,
中, ,
,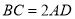 ,
,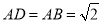 ,
,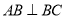 ,如图把
,如图把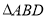 沿
沿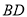 翻折,使得平面
翻折,使得平面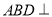 平面
平面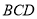 .
.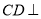 平面
平面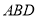 ;
;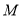 为线段
为线段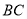 中点,求点
中点,求点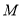 到平面
到平面 的距离.
的距离.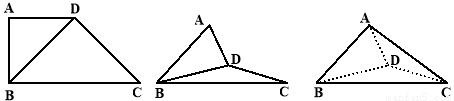
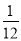 B.
B. C.
C. D.
D.