题目内容
数列{an}满足a1=1,且对任意的m,n∈N*,都有am+n=am+an+mn,则 +
+ +
+ +…+
+…+ =( )
=( )
 +
+ +
+ +…+
+…+ =( )
=( )A.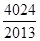 | B. | C. | D. |
B
令m=1得an+1=an+n+1,
即an+1-an=n+1,
于是a2-a1=2,a3-a2=3,…,an-an-1=n(n≥2),
上述n-1个式子相加得an-a1=2+3+…+n,
所以an=1+2+3+…+n=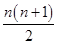 ,
,
当n=1时,a1=1满足上式,
所以an=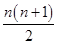 (n∈N*),
(n∈N*),
因此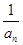 =
=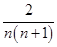 =2(
=2(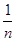 -
-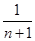 ),
),
所以 +
+ +
+ +…+
+…+
=2(1-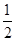 +
+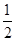 -
-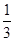 +…+
+…+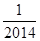 -
-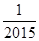 )
)
=2(1-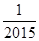 )
)
=
即an+1-an=n+1,
于是a2-a1=2,a3-a2=3,…,an-an-1=n(n≥2),
上述n-1个式子相加得an-a1=2+3+…+n,
所以an=1+2+3+…+n=
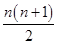 ,
,当n=1时,a1=1满足上式,
所以an=
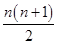 (n∈N*),
(n∈N*),因此
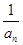 =
=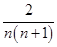 =2(
=2(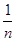 -
-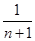 ),
),所以
 +
+ +
+ +…+
+…+
=2(1-
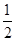 +
+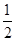 -
-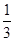 +…+
+…+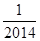 -
-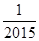 )
)=2(1-
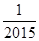 )
)=


练习册系列答案
相关题目
 的前
的前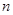 项和为
项和为 ,且对任意正整数
,且对任意正整数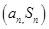 都在直线
都在直线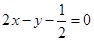 上.求数列
上.求数列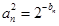 设
设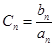 求:数列
求:数列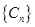 前
前 .
.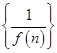 (n∈N*)的前n项和是( )
(n∈N*)的前n项和是( )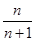
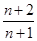
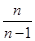
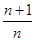
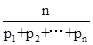 为
为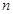 个正数
个正数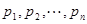 的“均倒数”.若已知数列
的“均倒数”.若已知数列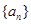 的前
的前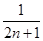 ,又
,又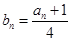 ,则
,则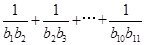 =( )
=( )



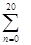 (1+2n)=________.
(1+2n)=________.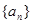 的前
的前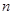 项和为
项和为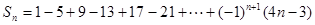 ,则
,则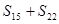 的值是( )
的值是( )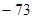
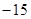
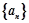 的通项公式为
的通项公式为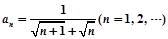 ,
,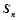 是数列
是数列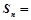 ( )
( )


