Question

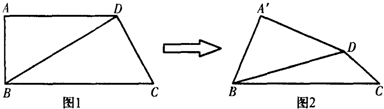（2013•许昌二模）在直角梯形ABCD中，AD∥BC，AB=1，AD=

3

，AB⊥BC，CD⊥BD，如图1，把△ABD沿BD翻折，使得平面A'BD⊥平面BCD，如图2．
（Ⅰ）求证：CD⊥A'B；
（Ⅱ）求三棱锥A'-BDC的体积．

Answer 1

分析：（Ⅰ）利用平面A′BD⊥平面BCD，根据面面垂直的性质，可得CD⊥平面A′BD，利用线面垂直的性质，可得CD⊥A′B；
（Ⅱ）作出三棱锥的高，利用三棱锥的体积公式，可求三棱锥A'-BDC的体积．

解答：（Ⅰ）证明：∵平面A′BD⊥平面BCD，平面A′BD∩平面BCD=BD，CD⊥BD，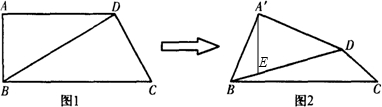
∴CD⊥平面A′BD，
∵AB?平面A′BD
∴CD⊥A′B；
（Ⅱ）解：如图1，在Rt△ABD中，BD=

AB2+AD2

=2
∵AD∥BC，∴∠ADB=∠DBC=30°
在Rt△BDC中，DC=BDtan30°=

2 3

3

∴S_△BDC=

1

2

BD•DC=

2 3

3

如图2，在Rt△A′BD中，过点A′作A′E⊥BD于E，则A′E⊥平面BCD
∵A′E=

A′B•A′D

BD

=

3

2

∴V_A′-BDC=

1

3

S△BDC•A′E=

1

3

•

2 3

3

•

3

2

=

1

3

点评：本题考查面面垂直、线面垂直的性质，考查三棱锥体积的计算，考查学生分析解决问题的能力，掌握面面垂直、线面垂直的性质是解题的关键．