题目内容
已知数列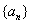 的前
的前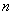 项和
项和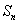 ,满足:
,满足: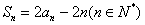
(1)求证: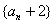 是等比数列
是等比数列
(2)求数列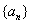 的通项
的通项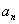
(3)若数列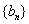 的满足
的满足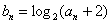 ,
,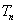 为数列
为数列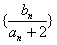 的前
的前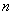 项和,求证
项和,求证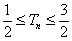
(1)证明:当 时,
时,  ,则当
,则当 时,
时,
两式相减得 ,即
,即
 ,
, ,
,
当 时,
时, ,则
,则
 是以
是以 为首项,2为公比的等比数列-
为首项,2为公比的等比数列-
(2)解:由(1)可知, ,
,
(3)证明: ,
, -
-
则 ①
①  ②
②


练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目

 是方程
是方程 的两根,则
的两根,则
 是第一象限角,且
是第一象限角,且
 的值
的值 的值
的值 在
在 处的切线的斜率为 .
处的切线的斜率为 .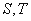 是
是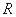 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从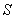 到
到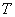 的函数
的函数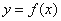 满足:
满足: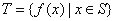 ;(ii)对任意
;(ii)对任意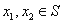 ,当
,当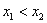 时,恒有
时,恒有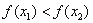 .
.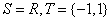 ;
;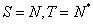 ;
;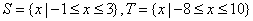 ;
;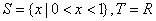
 的前n项和为
的前n项和为 ,若
,若 ,
, ,则
,则 ___________
___________  为等差数列,
为等差数列, 为等比数列,
为等比数列, ,则
,则 .
.