题目内容
求半径为4，与圆x2＋y2―4x―2y―4＝0相切，且和直线y＝0相切的圆的方程．
解：由题意，所求圆与直线y＝0相切，且半径为4，
则圆心坐标为O1(a，4)，O1(a，－4)．
又已知圆x2＋y2―4x―2y―4＝0的圆心为O2(2，1)，半径为3，
①若两圆内切，则|O1O2|＝4－3＝1．
即(a－2)2＋(4－1)2＝12，或(a－2)2＋(－4－1)2＝12．
显然两方程都无解．
②若两圆外切，则|O1O2|＝4＋3＝7．
即(a－2)2＋(4－1)2＝72，或(a－2)2＋(－4－1)2＝72．
解得a＝2±2
，或a＝2±2
．
∴所求
圆的方程为
(x―2―2)2＋(y－4)2＝16或(x－2＋2)2＋(y－4)2＝16；
或(x―2―2)2＋(y＋4)2＝16或(x―2＋2)2＋(y＋4)2＝16．
练习册系列答案
相关题目
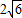，求圆C的方程．
，求圆C的方程．